数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学使用C++查找给定点可以构成四边形的数量
在欧几里得平面几何中，四边形是由四个顶点和四条边组成的多边形。名称4-gon等包含在四边形的其他名称中，有时它们也被称为正方形、显示样式等。
在本文中，我们将解释从给定点查找可能四边形数量的方法。在这个问题中，我们需要找出使用笛卡尔平面中提供的四个点(x, y)可以创建多少个可能的四边形。以下是给定问题的示例：
Input : A( -2, 8 ), B( -2, 0 ), C( 6, -1 ), D( 0, 8 ) Output : 1 Explanation : One quadrilateral can be formed ( ABCD )
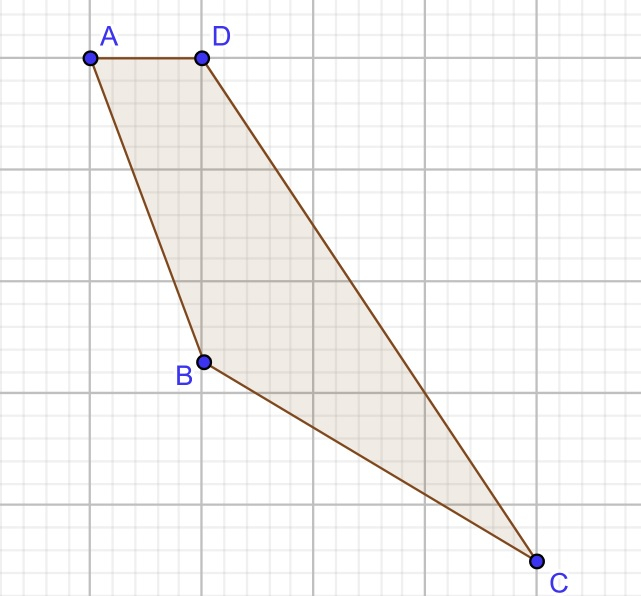
Input : A( 1, 8 ), B( 0, 1 ), C( 4, 0 ), D( 1, 2 ) Output : 3 Explanation : 3 quadrilaterals can be formed (ABCD), (ABDC) and (ADBC).
寻找解决方案的方法
我们将首先检查4个点中的3个是否共线，如果是，则**无法用这些点构成四边形**。
之后，我们将检查4个点中的任意2个是否相同，如果是，则**无法构成四边形**。
现在，我们将检查对角线是否相交。如果相交，则只能**构成一个可能的四边形**，称为**凸四边形**。
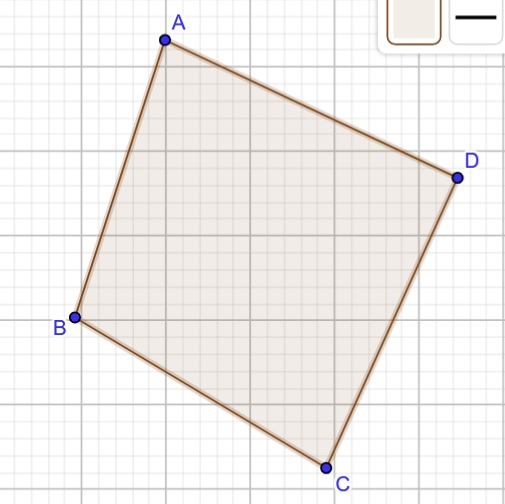
相交总数 = 1
如果对角线不相交，则可以构成三个可能的四边形，称为凹四边形。
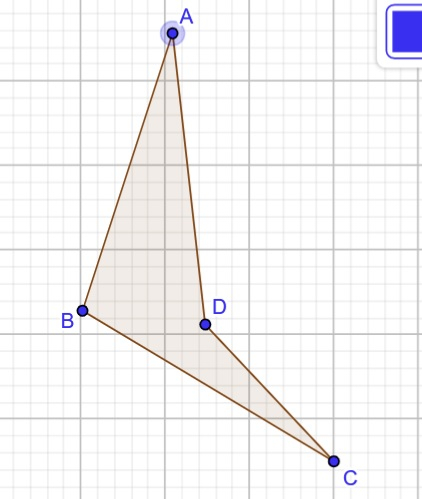
相交总数 = 0
示例
#include <iostream>
using namespace std;
struct Point{ // points
int x;
int y;
};
int check_orientation(Point i, Point j, Point k){
int val = (j.y - i.y) * (k.x - j.x) - (j.x - i.x) * (k.y - j.y);
if (val == 0)
return 0;
return (val > 0) ? 1 : 2;
}
// checking whether line segments intersect
bool check_Intersect(Point A, Point B, Point C, Point D){
int o1 = check_orientation(A, B, C);
int o2 = check_orientation(A, B, D);
int o3 = check_orientation(C, D, A);
int o4 = check_orientation(C, D, B);
if (o1 != o2 && o3 != o4)
return true;
return false;
}
// checking whether 2 points are same
bool check_similar(Point A, Point B){
// If found similiar then we are returning false that means no quad. can be formed
if (A.x == B.x && A.y == B.y)
return false;
// returning true for not found similiar
return true;
}
// Checking collinearity of three points
bool check_collinear(Point A, Point B, Point C){
int x1 = A.x, y1 = A.y;
int x2 = B.x, y2 = B.y;
int x3 = C.x, y3 = C.y;
if ((y3 - y2) * (x2 - x1) == (y2 - y1) * (x3 - x2))
return false;
else
return true;
}
// main function
int main(){
struct Point A,B,C,D;
A.x = -2, A.y = 8;// A(-2, 8)
B.x = -2, B.y = 0;// B(-2, 0)
C.x = 6, C.y = -1;// C(6, -1)
D.x = 0, D.y = 8;// D(0, 8)
// Checking whether any 3 points are collinear
bool flag = true;
flag = flag & check_collinear(A, B, C);
flag = flag & check_collinear(A, B, D);
flag = flag & check_collinear(A, C, D);
flag = flag & check_collinear(B, C, D);
// If points found collinear
if (flag == false){
cout << "Number of quadrilaterals possible from the given points: 0";
return 0;
}
// Checking if 2 points are same.
bool same = true;
same = same & check_similar(A, B);
same = same & check_similar(A, C);
same = same & check_similar(B, D);
same = same & check_similar(C, D);
same = same & check_similar(A, D);
same = same & check_similar(B, C);
// If similiar point exist
if (same == false){
cout << "Number of quadrilaterals possible from the given points: 0";
return 0;
}
// checking whether diagonal intersect or not
flag = true;
if (check_Intersect(A, B, C, D))
flag = false;
if (check_Intersect(A, C, B, D))
flag = false;
if (check_Intersect(A, B, D, C))
flag = false;
if (flag == true)
cout << "Number of quadrilaterals possible from the given points: 3";
else
cout << "Number of quadrilaterals possible from the given points: 1";
return 0;
}输出
Number of quadrilaterals possible from the given points : 1
以上代码的解释
此代码可以通过以下步骤理解：
检查是否有三个点共线，如果是，则四边形的数量：0
检查是否有两个点相同，如果是，则四边形的数量：0
检查是否有任何线段相交
如果是，则四边形的数量：1
如果不是，则四边形的数量：3
结论
在本文中，我们解决了从给定的4个点中找到所有可能的四边形的问题。我们了解四边形的数量如何取决于共线性、相交和方向。我们还为此编写了C++程序，我们也可以用其他语言（如C、Java和Python）编写此程序。
更新于：2021年11月24日
360 次浏览
广告