全波整流器

全波整流器是一种二极管电路，用于将交流电压（交流电源）的完整周期转换为直流电压（直流电源）。

在全波整流中，电流在交流电源的整个周期内都沿相同方向流过负载。

全波整流器的类型

• 中心抽头全波整流器
• 桥式全波整流器

中心抽头全波整流器

中心抽头全波整流器的电路包含以下主要组件：

• 两个二极管
• 一个中心抽头变压器
• 一个负载电阻

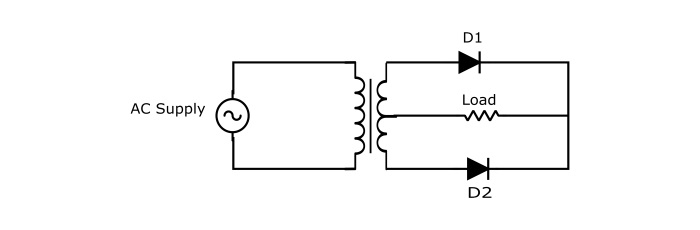
中心抽头全波整流器电路的工作原理

正半周期

在输入交流电压的正半周期内，次级绕组的A端为正，B端为负。这使得二极管D1正向偏置（像闭合开关一样），二极管D2反向偏置（像断开开关一样）。因此，电流从P点流经负载（RL）到O点。

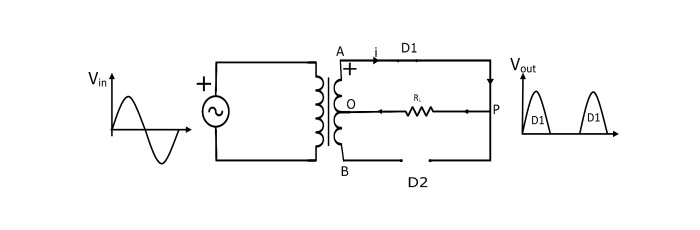
负半周期

在输入交流电源的负半周期内，次级绕组的B端为正，A端为负。这使得二极管D2正向偏置（像闭合开关一样），二极管D1反向偏置（像断开开关一样）。因此，电流将从B点流经二极管D2、负载RL和次级绕组的下半部分到O点。

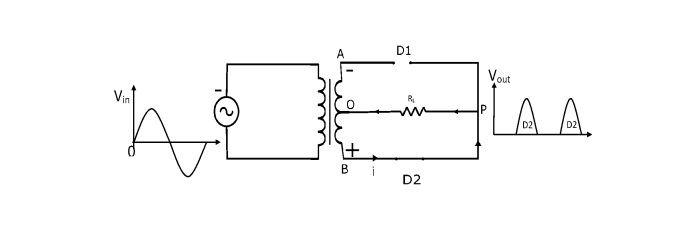
请注意，负载电流在输入交流电源的两个半周期内方向相同。因此，在负载上获得直流输出。

中心抽头全波整流器的输出频率

输出频率是输入频率的两倍。由于输入电源是每2π弧度重复一次的正弦波。全波整流器的输出是脉动的直流电，每2π弧度内重复输入交流电的相同模式两次。

$$\mathrm{f_{out}=2f_{in}}$$

中心抽头全波整流器的缺点

• 二极管必须具有峰值反向电压。
• 很难在次级绕组上找到中心抽头。

桥式全波整流器

桥式全波整流器消除了对中心抽头变压器的需求。它包含四个连接成桥的二极管。

桥式全波整流器的电路图

桥式全波整流器的电路包含以下主要组件：

• 四个二极管
• 一个降压变压器
• 一个负载电阻

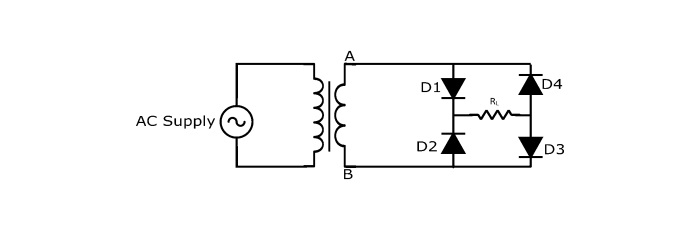
桥式全波整流器的电路工作原理

正半周期

在正半周期内，次级绕组的A端为正，B端为负。这使得二极管D1和D3正向偏置（像闭合开关一样），二极管D2和D4反向偏置（像断开开关一样）。电流从A点流经二极管D1、负载RL和二极管D3到B点。

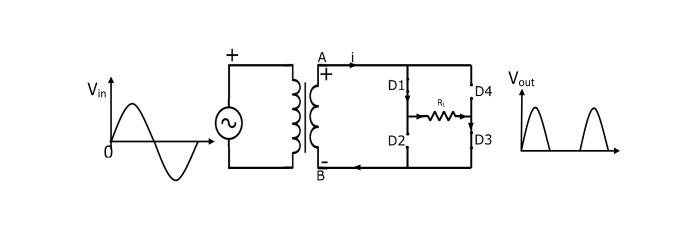
负半周期

在负半周期内，次级绕组的A端为负，B端为正。这使得二极管D1和D3反向偏置（像断开开关一样），二极管D2和D4正向偏置（像闭合开关一样）。电流从B点流经二极管D2、负载RL和二极管D4到A点。

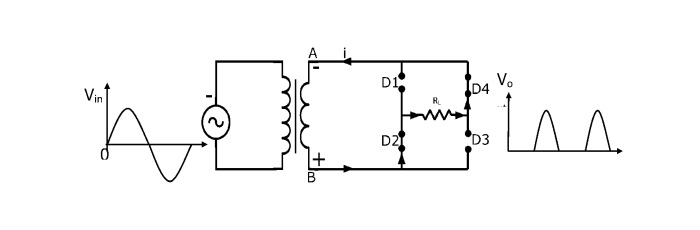
因此，电流在输入交流电源的两个周期内都沿相同方向流过负载RL。因此，在负载上获得直流输出。

桥式全波整流器的优点

• 对于相同的次级电压，输出是中心抽头全波整流器的两倍。

• 不需要中心抽头变压器。

• 对于相同的直流输出，桥式全波整流器的PIV是中心抽头全波整流器的一半。

桥式全波整流器的缺点

• 它需要四个二极管。

• 在交流输入的每个半周期内，导通的两个二极管串联，这会导致二极管内阻压降。

全波整流器波形

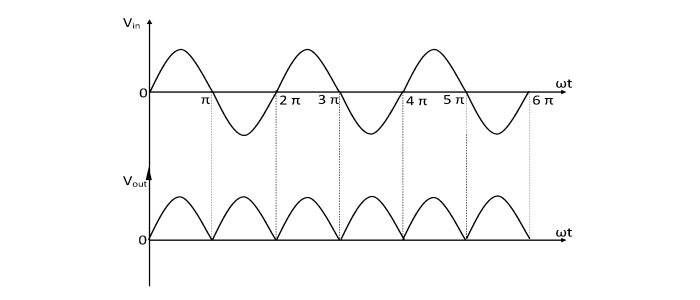
全波整流器公式

全波整流器的效率

全波整流器的效率定义为直流输出功率与交流输入功率之比。

$$\mathrm{\eta=\frac{P_{dc}}{P_{ac}}}$$

全波整流器的最大效率为81.2%。

全波整流器的峰值反向电压

“PIV是二极管在反向偏置时可以承受的最大电压，超过此电压将导致二极管损坏。”

• 对于中心抽头全波整流器，PIV是最大次级绕组电压的两倍。

$$\mathrm{PIV=2V_{m}}$$

• 对于桥式全波整流器，每个二极管的PIV等于最大次级电压。

$$\mathrm{PIV=V_{m}}$$

全波整流器负载电流的有效值

$$\mathrm{I_{RMS}=\frac{I_{m}}{\sqrt{2}}}$$

全波整流器负载电流的平均值

$$\mathrm{I_{RMS}=\frac{2I_{m}}{\pi}}$$

全波整流器的直流输出电压

$$\mathrm{V_{dc}=V_{dc}R_{L}=V_{avg}R_{L}}$$

全波整流器的波形系数

$$\mathrm {{波形系数}=\frac{有效值}{平均值}=\frac{V_{rms}}{V_{avg}}}$$

对于全波整流器，波形系数等于1.11。

全波整流器的纹波系数

纹波系数提供了关于全波整流器如何将交流输入电压转换为直流输出电压的信息。它由下式给出：

$$\mathrm{纹波系数=\sqrt{(波形系数)^2}-1}$$

全波整流器的纹波系数为0.482。

数值例题 #1

在一个中心抽头全波整流器中，每个二极管的内阻为。从中心抽头到次级绕组每一端的变压器次级有效电压为60 V，负载电阻为。求：

• 平均负载电流
• 负载电流的有效值
• 直流输出电压
• 峰值反向电压

解答

次级绕组半边的有效电压，V_rms=60V

次级绕组半边的最大电压，$V_{m}=60×\sqrt{2}=84.84 V$

$$\mathrm{(∵ V_{m}=V_{rms}×√2 )}$$

$$\mathrm{I_{m}=\frac{V_{m}}{R_{d}+R_{L}}=\frac{84.84}{(10+870)}=96.41 mA}$$

(a) 平均负载电流

$$\mathrm{I_{avg}=\frac{2I_{m}}{\pi}=\frac{2×96.41}{\pi}=61.41 mA}$$

(b) 负载电流的有效值

$$\mathrm{I_{rms}=\frac{I_{m}}{\sqrt{2}}=\frac{96.41}{\sqrt{2}}=68.18 mA}$$

(c) 直流输出电压

$$\mathrm{V_{dc}=I_{avg}R_{L}=61.41×870=53.43 V}$$

(d) 峰值反向电压

$$\mathrm{PIV=2V_{m}=2×84.84=169.68 V}$$

数值例题 #2

在一个桥式全波整流器电路中，每个二极管的正向电阻为2Ω，反向电阻为无穷大。交流电源电压为230 V有效值，负载电阻为50Ω。计算：

• (a) 平均负载电流
• (b) 整流器效率

解答

电源电压的有效值

$$\mathrm{V_{rms}=230 V}$$

电源电压的最大值

$$\mathrm{V_{m}=230×√2=325.22 V}$$

负载电流的最大值

$$\mathrm{I_{m}=\frac{V}{2R_{d}+R_{L}}=\frac{325.22}{(4+50)}=6.02 A}$$

(a) 平均负载电流

$$\mathrm{I_{avg}=\frac{2I_{m}}{\pi}=\frac{2×6.02}{\pi}=3.83 A}$$

(b) 负载电流的有效值

$$\mathrm{I_{rms}=\frac{I_{m}}{\sqrt{2}}=\frac{6.02}{\sqrt{2}}=4.26 A}$$

整流器效率，

$$\mathrm{\eta=\frac{P_{dc}}{P_{ac}}=\frac{I_{avg}^2×R_{L}}{(I_{rms})^2×(2R_{d}+R_{L})}=\frac{3.83^2×50}{4.26^2×54}×100=74.84\%}$$

Saini Manish Kumar

更新于：2023年11月3日

27K+ 浏览量

启动您的职业生涯

完成课程获得认证

开始学习