数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学如何进行 Z 检验：双样本均值？
在本文中，我们将学习如何在 MS Excel 中对两个独立样本进行 Z 检验。Z 检验的主要目标是检验两个独立样本的均值。借助 MS Excel 内置的数据分析选项，用户可以通过 Z 检验找到汇总值，并得出是否拒绝零假设或接受零假设的结论，用户在执行 Z 检验后利用 p 值。
零假设 - 心脏病患者和高血压患者的平均值之间没有显著差异
备择假设 - 心脏病患者和高血压患者的平均值之间存在显著差异。
进行双样本 Z 检验
考虑描述居住在不同城市的患心脏病患者人数和患高血压患者人数的样本数据集。
步骤 1 - 在工作表中创建数据集，第一列表示多个城市的名称，第二列包含包含心脏病患者人数的第一个样本数据，第三列表示代表高血压患者人数的第二个样本信息。在应用 Z 检验之前，我们必须计算不同样本的方差。
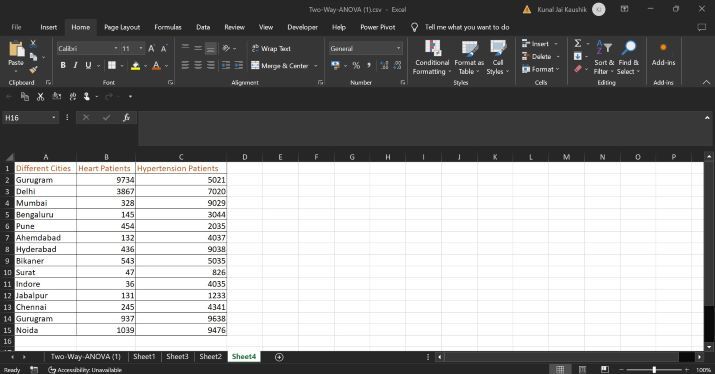
步骤 2 - 计算第一个样本的方差。在 B17 单元格中写入公式=VAR.S(B2:B15)，如下所示：
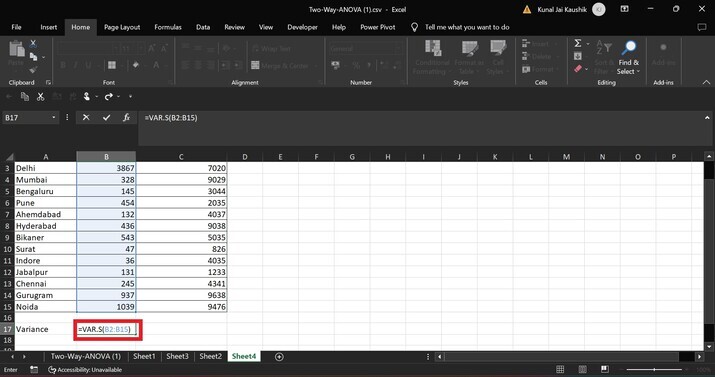
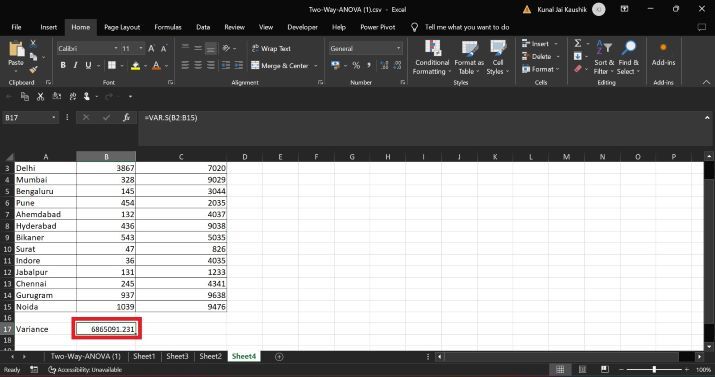
然后按Enter键获取指定数据集的方差。
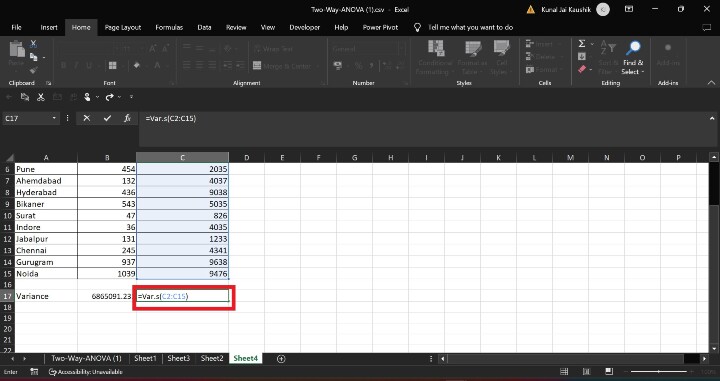
步骤 3 - 同样，计算第二个样本的方差。输入方差公式=VAR.S(C2:C15) 并按Enter 键。
步骤 4 - 从数据选项卡中选择名为数据分析的选项，如下图所示：
步骤 5 - 将出现另一个名为数据分析的对话框。从该对话框的下拉菜单中选择Z 检验：双样本均值，然后按确定按钮。
步骤 6 - 在变量 1 区域和变量 2 区域标签的前面分别写入第一个数据集和第二个数据集的范围。输入我们在步骤 2 和步骤 3 中计算的方差 1 和方差 2 的值。将 Alpha 值设置为 0.05。在输出选项部分，用户可以选择任何选项。在这里，我们选择新建工作表 Ply: 选项，这意味着输出将在新工作表中生成。
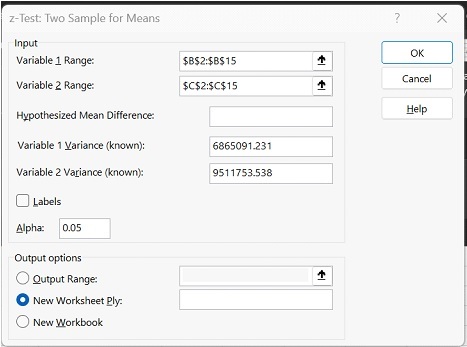
步骤 7 - 因此，输出显示在新工作表“sheet 5”中。
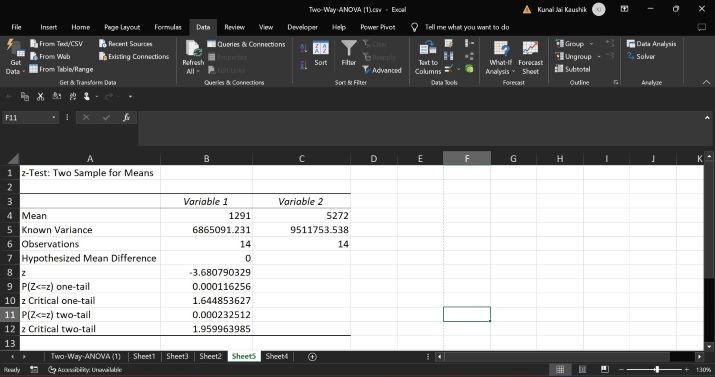
观察 Z 检验表后，单尾 P(Z<=z) 值 0.000116256 小于 0.05，双尾 P(Z<=z) 值 0.00023512 也小于 0.05，这意味着我们必须接受备择假设并拒绝零假设。
结论
有效的假设检验是使用 Excel 的一种重要方法，尤其是在处理大型复杂数据集时。通过利用 Excel 的内置数据分析选项（如 ANOVA、Z 检验、样本均值的 T 检验以及各种回归和相关方法），您可以快速获得和分析结果，而不会浪费时间。将这些技术融入您的工作流程中，以提高您的生产力，并使您的 Excel 体验更加流畅和愉快。
426 次浏览
