数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究N元树的同构
同构定义为两棵树具有相同的或镜像结构。在镜像结构的情况下，左节点数据将始终与右节点匹配。例如，我们将取最接近镜像的数字，看看它的反转是什么，这就是同构的真正概念。
在本文中，我们将检查两棵不同的二叉树是否同构。
让我们来看一个N元树同构的例子：
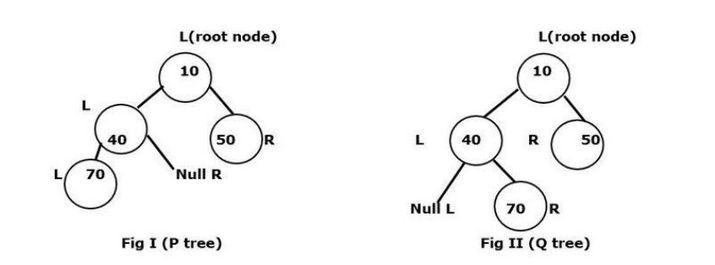
请注意，L 代表左节点，而 R 代表右节点
P 和 Q 树在最左边的第二个分区的镜像结构
这两个图显示了它们如何通过给出四个匹配条件（P 和 Q 的根节点）而彼此同构，例如：
左左节点可以匹配。
右右节点可以匹配。
左右节点可以匹配。
右左节点可以匹配。
语法
程序中使用的以下语法：
struct name_of_structure{
data_type var_name;
// data member or field of the structure.
}
参数
struct - 此关键字用于表示结构数据类型。
name_of_structure - 我们为结构提供任何名称。
结构是在一个地方收集各种相关变量。
算法
我们将从名为'iostream'的头文件开始程序。
我们正在创建一个名为'tree_node'的结构，其整数类型为'd'，并初始化指针变量'l'和'r'分别代表左子节点和右子节点数据。
现在我们创建另一个结构，其中包含一个名为'create_node()'的函数，该函数接受一个名为'data'的参数来处理根节点的值。此外，我们使用给定的数据创建'tree_node'指针来将左子节点和右子节点指针初始化为null，并返回根节点。使用此函数，我们将插入左子节点和右子节点。
我们正在创建一个布尔类型函数'check_isomorphism_tree'，以两个tree_node指针p和q作为输入参数并返回布尔值。在其中，我们创建两次“if 语句”来检查p中的数据是否等于q。
检查 p 和 q 是否都为 null，如果是，则返回 true，因为树是同构的。
检查 p 或 q 是否为 null，如果是，则返回 false，因为树不是同构的。
在'check_isomorphism_tree'函数中，我们使用逻辑运算符“&&”和“||”递归地检查节点'p'和'q'的左子节点和右子节点的所有可能组合。
我们从主函数开始，创建两个树节点'p'和'q'来提供信息。
在主函数中，我们使用 if 语句调用'check_isomorphism_tree'函数，并将给定的参数 p 和 q 传递给它，以验证这些整数值是否同构。如果它是同构的，则打印语句为“给定的节点信息将构成同构树”，否则反之。
示例
在这个程序中，我们将检查两棵二叉树是否同构。
#include<iostream>
using namespace std;
struct tree_node{
int d;
tree_node*l; // l = left
tree_node*r; // r = right
};
struct tree_node* create_node(int data){
struct tree_node*root= new tree_node;
root->d= data;
root->l= NULL;
root->r= NULL;
return root;
}
bool check_isomorphism_tree(tree_node*p, tree_node*q) {
// p and q both are different tree
if(p==NULL and q==NULL){
return true;
}
if(p==NULL or q==NULL){
return false;
}
// return all the possible condition
return (p->d==q->d && ((check_isomorphism_tree(p->l,q->r)&& check_isomorphism_tree(p->r,q->l))||(check_isomorphism_tree(p->l,q->l)&& check_isomorphism_tree(p->r,q->r))));
}
int main(){
// Tree of root p
struct tree_node *p = create_node(10);
p->l = create_node(5);
p->r = create_node(4);
p->l->l = create_node(11);
p->r->r = create_node(12);
p->l->r = create_node(51);
p->r->l = create_node(6);
p->l->r->l = create_node(7); // left->right->left
p->l->l->l = create_node(9); // left->left->left
// Tree of root q
struct tree_node *q = create_node(10);
q->l = create_node(5);
q->r = create_node(4);
q->l->l = create_node(11);
q->r->r = create_node(12);
q->l->r = create_node(51);
q->r->l = create_node(6);
q->l->r->l = create_node(7);
q->l->l->l = create_node(9);
if(check_isomorphism_tree(p,q)){
cout<<"This given information of node will make isomorphism tree"<<endl;
} else {
cout<<" This given information of node will not make isomorphism tree "<<endl;
}
return 0;
}
输出
This given information of node will make isomorphism tree
结论
在这个程序中，我们理解了 N 元树同构的概念。我们看到了结构如何帮助表示树节点，以及左左节点、右左节点、左右左节点等的使用如何帮助构建树，以及以下操作如何满足树的同构性。
379 次浏览
