图同构和同态

同构

如果两个图 G 和 H 含有数量相等的顶点并且连接方式相同，则称两个图是同构图 (表示为 G ≅ H)。

检查非同构比同构容易。如果发生以下任一条件，则两个图是非同构的 −

• 连通分量的数量不同
• 顶点集合势不同
• 边集合势不同
• 度序列不同

示例

以下图是同构图 −

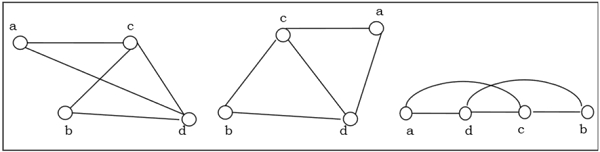
同态

从图 G 到图 H 的同态是一种映射 (可能不是双射映射) h: G → H，使得 − (x, y) ∈ E(G) → (h(x), h(y)) ∈ E(H)。它将图 G 的相邻顶点映射到图 H 的相邻顶点。

同态的特性

• 如果同态是双射映射，则同态是同构。

• 同态始终保留图的边和连通性。

• 同态的复合也是同态。

• 找出是否存在另一个图的同态图是一个 NP 完全问题。

Mahesh Parahar

更新于: 2019 年 8 月 23 日

7 千次以上浏览

职业生涯进阶

通过完成课程获得认证

开始