哈密顿图

哈密顿图 - 如果存在一个环包含图 G 的每个顶点并且该环称为哈密顿环，那么连通图 G 被称为哈密顿图。图 G 中的哈密顿路径是恰好经过每个顶点一次的路径。

狄拉克定理 - 如果 G 是一个具有 n 个顶点的简单图，其中 n ≥ 3 并且对于每个顶点 v，deg(v) ≥ {n}/{2}，那么图 G 是哈密顿图。

奥尔定理 - 如果 G 是一个具有 n 个顶点的简单图，其中 n ≥ 2 并且对于每个不相邻的顶点 x 和 y，deg(x) + deg(y) ≥ n，那么图 G 是哈密顿图。

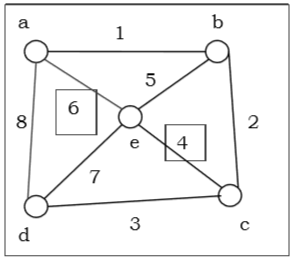
在上面的示例中，顶点 a 和 c 的度之和为 6，大于总顶点数 5，使用奥尔定理，它是一个哈密顿图。

非哈密顿图

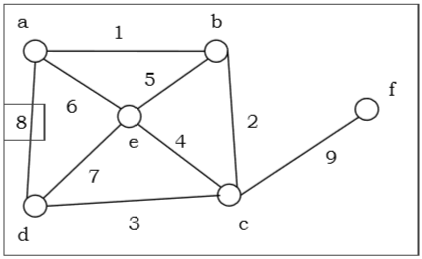
在上面的示例中，顶点 a 和 f 的度之和为 4，小于总顶点数 4，使用奥尔定理，它不是哈密顿图。

Mahesh Parahar

更新时间： 2019 年 8 月 23 日

14K+ 浏览量

开启你的 职业生涯

通过完成课程取得认证

立即开始