欧拉图

欧拉图 - 一个连通图 G 称为一个欧拉图，如果存在一个封闭的路径覆盖了图 G 的每条边。

欧拉路径 - 一个欧拉路径是一条只使用了一次图中每条边的路径。一条欧拉路径开始和结束于不同的顶点。

欧拉回路 - 一个欧拉回路是一条只使用了一次图中每条边的回路。一条欧拉回路始终开始和结束于相同的顶点。一个连通图 G 是一个欧拉图当且仅当图 G 的所有顶点的度数都是偶数，并且一个连通图 G 是欧拉图当且仅当它的边集可以分解成若干个环。

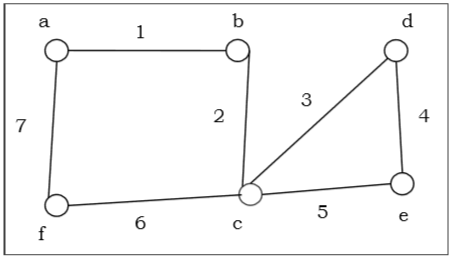
上面的图是一个欧拉图，因为一条路径 1 b 2 c 3 d 4 e 5 c 6 f 7 g 覆盖了图的所有边。

非欧拉图

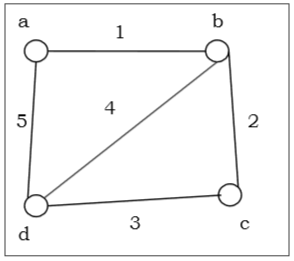
此处顶点 b 和 d 的度数为 3，是一个奇数度数，违反了欧拉图条件。

Mahesh Parahar

更新于： 2019 年 8 月 23 日

25K+ 浏览量

启动您的 职业生涯

通过完成课程获得认证

开始