数据结构
网络连接
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会学
时尚研究
法律研究Fleury 的算法在 C++ 中用于打印欧拉路径或欧拉环
Fleury 的算法用于显示给定图中的欧拉路径或欧拉环。在此算法中，从一条边开始，它尝试通过删除先前的顶点来移动其他相邻顶点。使用此技巧后，此图中的每个步骤都会变得简单，便于查找欧拉路径或欧拉环。
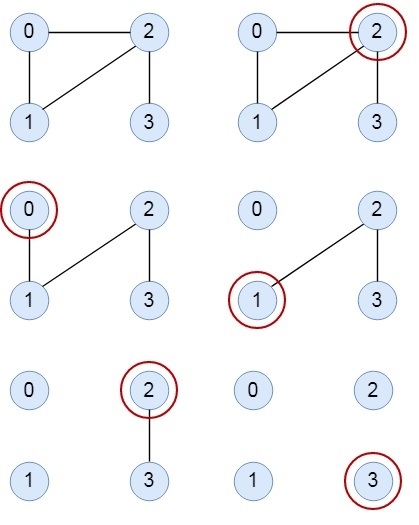
我们必须检查一些规则才能获得路径或环指示： -
- 此图必须是欧拉图。
- 当有两条边时，一条是桥，另一条是非桥时，我们必须首先选择非桥。
选择起点也很重要，我们不能将任何顶点用作起点，如果此图没有奇偶度顶点，则可以选择任何顶点作为起点，否则当一个顶点具有奇偶度时，我们必须首先选择它。
输入 - 图的邻接矩阵
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
输出 - 欧拉路径或欧拉环： 1--0 0--2 2--1 1--3 3--0 0--4 4--3 3--2
操作
findStartVert(graph) Input: The given graph. Output: Find the starting vertex to start algorithm. Begin for all vertex i, in the graph, do deg := 0 for all vertex j, which are adjacent with i, do deg := deg + 1 done if deg is odd, then return i done when all degree is even return 0 End isBridge(u, v) Input: The start and end node. Output: True when u and v are forming a bridge. Begin deg := 0 for all vertex i which are adjacent with v, do deg := deg + 1 done if deg > 1, then return false return true End fleuryAlgorithm(start) Input: The starting vertex. Output: Display the Euler path or circuit. Begin edge := get the number of edges in the graph //it will not initialize in next recursion call for all vertex v, which are adjacent with start, do if edge <= 1 OR isBridge(start, v) is false, then display path from start and v remove edge (start,v) from the graph decrease edge by 1 fleuryAlgorithm(v) done End
示例
#include<iostream>
#include<vector>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {{0, 1, 1, 1, 1},
{1, 0, 1, 1, 0},
{1, 1, 0, 1, 0},
{1, 1, 1, 0, 1},
{1, 0, 0, 1, 0}
};
int tempGraph[NODE][NODE];
int findStartVert(){
for(int i = 0; i<NODE; i++){
int deg = 0;
for(int j = 0; j<NODE; j++){
if(tempGraph[i][j])
deg++; //increase degree, when connected edge found
}
if(deg % 2 != 0) //when degree of vertices are odd
return i; //i is node with odd degree
}
return 0; //when all vertices have even degree, start from 0
}
bool isBridge(int u, int v){
int deg = 0;
for(int i = 0; i<NODE; i++)
if(tempGraph[v][i])
deg++;
if(deg>1){
return false; //the edge is not forming bridge
}
return true; //edge forming a bridge
}
int edgeCount(){
int count = 0;
for(int i = 0; i<NODE; i++)
for(int j = i; j<NODE; j++)
if(tempGraph[i][j])
count++;
return count; //count nunber of edges in the graph
}
void fleuryAlgorithm(int start){
static int edge = edgeCount();
for(int v = 0; v<NODE; v++){
if(tempGraph[start][v]){ //when (u,v) edge is presnt and not forming bridge
if(edge <= 1 || !isBridge(start, v)){
cout << start << "--" << v << " ";
tempGraph[start][v] = tempGraph[v][start] = 0; //remove edge from graph
edge--; //reduce edge
fleuryAlgorithm(v);
}
}
}
}
int main(){
for(int i = 0; i<NODE; i++) //copy main graph to tempGraph
for(int j = 0; j<NODE; j++)
tempGraph[i][j] = graph[i][j];
cout << "Euler Path Or Circuit: ";
fleuryAlgorithm(findStartVert());
}输出
Euler Path Or Circuit: 1--0 0--2 2--1 1--3 3--0 0--4 4--3 3—2
更新于： 25-9-2019
2K+ 次浏览
广告