数据结构中的欧拉图和哈密顿图

在本节中，我们将了解欧拉图和哈密顿图。但在深入探讨之前，我们首先需要了解图中的轨迹。假设我们有一个如下所示的图：

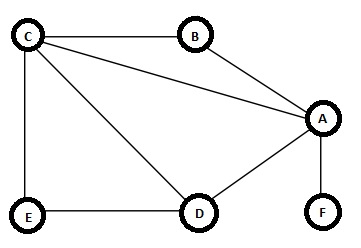
轨迹是一条路径，它是一系列边 (v1, v2), (v2, v3), …, (vk - 1, vk)，其中所有顶点 (v1, v2, … , vk) 可能不尽相同，但所有边都不同。在这个例子中，一个轨迹是 {(B, A), (A, C), (C, D), (D, A), (A, F)}。这是一个轨迹。但它不被认为是简单路径，因为顶点 A 被访问了两次。如果第一个和最后一个顶点相同，则它将是一个闭合轨迹。

欧拉迹

在图 G(V, E) 中，欧拉迹是指包含每条边恰好一次的轨迹。如果 G 具有闭合欧拉迹，则该图称为欧拉图。换句话说，我们可以说，如果从一个顶点开始，我们可以遍历每条边恰好一次并返回到起始顶点，则图 G 将是欧拉图。欧拉证明，当且仅当其每个顶点的度数均为偶数时，图才称为欧拉图。

哈密顿回路

如果一个回路经过图 G 的每个顶点，则该回路称为哈密顿回路。许多不同的定理给出了图成为哈密顿图的充分条件。然而，确定任意图是否为哈密顿图的问题是一个 NP 完全问题。

更新于：2020年8月10日

浏览量 1K+

开启您的职业生涯

完成课程获得认证

开始学习
广告