欧拉路径和哈密顿路径

如果可以在不重复相同路径的情况下，在所有顶点之间绘制一条路径，则该图是可遍历的。基于此路径，有一些类别，例如欧拉路径和欧拉回路，在本节中进行了描述。

欧拉路径

欧拉路径包含图“G”中的每条边恰好一次，并且包含图“G”中的每个顶点至少一次。如果连通图 G 包含欧拉路径，则称该图是可遍历的。

示例

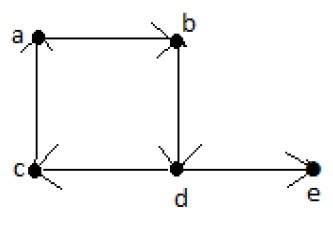
**欧拉路径** = d-c-a-b-d-e。

欧拉回路

在欧拉路径中，如果起始顶点与其结束顶点相同，则称为欧拉回路。

示例

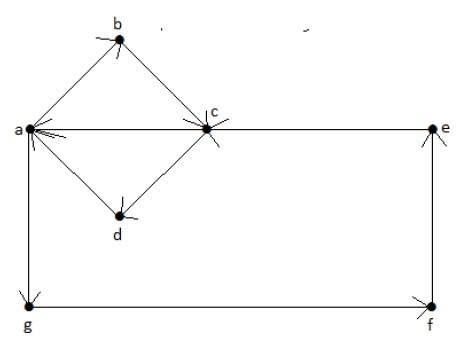
**欧拉路径** = a-b-c-d-a-g-f-e-c-a。

欧拉回路定理

连通图“G”是可遍历的当且仅当 G 中具有奇数度的顶点数恰好为 2 或 0。如果一个连通图 G 恰好有两个具有奇数度的顶点，则它可以包含欧拉路径，但不能包含欧拉回路。

**注意** - 此欧拉路径以一个奇数度顶点开始，以另一个奇数度顶点结束。

示例

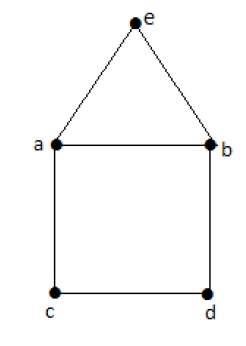
**欧拉路径** - b-e-a-b-d-c-a 不是欧拉回路，但它是欧拉路径。显然，它恰好有两个奇数度顶点。

**注意** - 在连通图 G 中，如果具有奇数度的顶点数 = 0，则存在欧拉回路。

哈密顿路径

如果一个连通图包含图 G 中的每个顶点恰好一次，则称该图是哈密顿图。这样的路径称为**哈密顿路径**。

示例

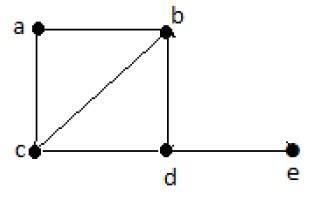
**哈密顿路径** - e-d-b-a-c。

**注意** -

• 欧拉回路包含图中每条边恰好一次。
• 在哈密顿回路中，可以跳过图中的一些边。

示例

请看下图 -

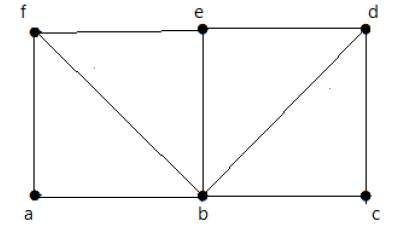
对于上面显示的图 -

• 存在欧拉路径 – 错误
• 存在欧拉回路 – 错误
• 存在哈密顿回路 – 正确
• 存在哈密顿路径 – 正确

G 有四个奇数度顶点，因此它不可遍历。通过跳过内部边，该图具有一个经过所有顶点的哈密顿回路。

Mahesh Parahar

更新于: 2019-08-23

8K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习