数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究在 C++ 中添加使欧拉回路所需的最小边数
概念
对于给定的具有 b 个节点和 a 条边的无向图，任务是确定在给定图中构建欧拉回路所需的最小边数。
输入
b = 3,
a = 2
Edges[] = {{1, 2}, {2, 3}}输出
1
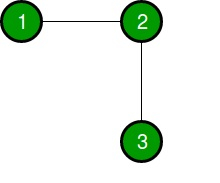
通过连接 1 到 3，我们可以构建一个欧拉回路。
方法
为了使图中存在欧拉回路，我们需要每个节点都具有偶数度，因为这样就存在一条可以用于在进入节点后离开节点的边。
现在，可能有两种情况：
图中存在一个连通分量
对于这种情况，如果图中所有节点都具有偶数度，那么我们说该图已经具有欧拉回路，我们不需要在其中添加任何边。但是，如果存在任何具有奇数度的节点，则我们需要添加边。图中可以存在偶数个奇数度顶点。这个事件可以通过偶数度节点的度数和奇数度节点的度数之和等于总度数这一事实轻松验证，总度数始终为偶数，因为每条边对这个和的贡献为 2。因此，如果我们将图中随机的奇数度节点配对并在它们之间添加一条边，我们就可以使所有节点都具有偶数度，从而使欧拉回路存在。
图中存在不连通分量
首先，我们将分量标记为奇数和偶数。奇数分量是指其中至少存在一个奇数度节点的分量。现在，我们取所有偶数分量，并从每个分量中选择一个随机顶点，并将它们线性排列。因此，在相邻顶点之间添加边，我们已经连接了偶数分量并构建了一个等效的奇数分量，该分量有两个奇数度节点。
因此，为了处理奇数分量，即至少存在一个奇数度节点的分量，我们可以使用边连接所有这些奇数分量，边的数量等于不连通分量的数量。这可以通过将分量按循环顺序放置并从每个分量中选择两个奇数度节点并将它们用于连接到两侧的分量来实现。现在我们有一个单个连通分量，我们已经对其进行了解释。
示例
//This C++ program finds minimum edge required
// to make Euler Circuit
#include <bits/stdc++.h>
using namespace std;
// This Depth-First Search finds a connected
// component
void dfs1(vector<int> g1[], int vis1[], int odd1[],
int deg1[], int comp, int v){
vis1[v] = 1;
if (deg1[v]%2 == 1)
odd1[comp]++;
for (int u : g1[v])
if (vis1[u] == 0)
dfs1(g1, vis1, odd1, deg1, comp, u);
}
// We return minimum edge required to build Euler
// Circuit
int minEdge1(int n, int m, int s1[], int d1[]){
// g1 : to store adjacency list
// representation of graph.
// e1 : to store list of even degree vertices
// o1 : to store list of odd degree vertices
vector<int> g1[n+1], e1, o1;
int deg1[n+1]; // Degrees of vertices used
int vis1[n+1]; // To store visited in DFS
int odd1[n+1]; // Number of odd nodes in components
memset(deg1, 0, sizeof(deg1));
memset(vis1, 0, sizeof(vis1));
memset(odd1, 0, sizeof(odd1));
for (int i = 0; i < m; i++){
g1[s1[i]].push_back(d1[i]);
g1[d1[i]].push_back(s1[i]);
deg1[s1[i]]++;
deg1[d1[i]]++;
}
// This 'ans' is result and 'comp' is component id
int ans = 0, comp = 0;
for (int i = 1; i <= n; i++){
if (vis1[i]==0){
comp++;
dfs1(g1, vis1, odd1, deg1, comp, i);
// We check that if connected component
// is odd.
if (odd1[comp] == 0)
e1.push_back(comp);
// We check that if connected component
// is even.
else
o1.push_back(comp);
}
}
// It has been seen that if whole graph is a single connected
// component with even degree.
if (o1.size() == 0 && e1.size() == 1)
return 0;
// It has been seen that if all connected component is even
if (o1.size() == 0)
return e1.size();
//It has been seen that if graph have atleast one even connected
// component
if (e1.size() != 0)
ans += e1.size();
// For all the odd connected component.
for (int i : o1)
ans += odd1[i]/2;
return ans;
}
// Driven Program
int main(){
int b = 3, a = 2;
int source1[] = { 1, 2 };
int destination1[] = { 2, 3 };
cout << minEdge1(b, a, source1, destination1) << endl;
return 0;
}输出
1
更新于：2020-07-23
196 次查看
广告