数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究所有节点对的最短路径
所有节点对最短路径算法也称为弗洛伊德-沃歇尔算法，用于在一个给定的加权图中查找所有节点对的最短路径问题。通过该算法，它将生成一个矩阵，该矩阵表示从任意节点到图中所有其他节点的最小距离。
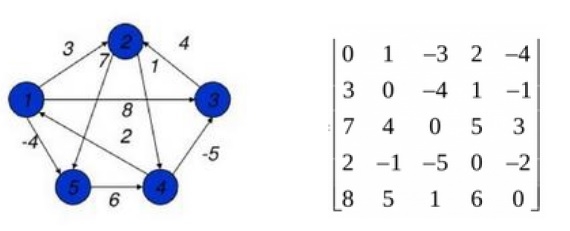
首先，输出矩阵与给定的图的成本矩阵相同。之后，输出矩阵将使用所有顶点 k 作为中间顶点进行更新。
该算法的时间复杂度为 O(V3)，其中 V 是图中顶点的数量。
输入 - 图的成本矩阵。
0 3 6 ∞ ∞ ∞ ∞ 3 0 2 1 ∞ ∞ ∞ 6 2 0 1 4 2 ∞ ∞ 1 1 0 2 ∞ 4 ∞ ∞ 4 2 0 2 1 ∞ ∞ 2 ∞ 2 0 1 ∞ ∞ ∞ 4 1 1 0
输出 - 所有节点对最短路径的矩阵。
0 3 4 5 6 7 7 3 0 2 1 3 4 4 4 2 0 1 3 2 3 5 1 1 0 2 3 3 6 3 3 2 0 2 1 7 4 2 3 2 0 1 7 4 3 3 1 1 0
算法
floydWarshal(cost)
输入 - 给定图的成本矩阵。
输出 - 任意顶点到任意顶点之间最短路径的矩阵。
Begin for k := 0 to n, do for i := 0 to n, do for j := 0 to n, do if cost[i,k] + cost[k,j] < cost[i,j], then cost[i,j] := cost[i,k] + cost[k,j] done done done display the current cost matrix End
示例
#include<iostream>
#include<iomanip>
#define NODE 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[NODE][NODE] = {
{0, 3, 6, INF, INF, INF, INF},
{3, 0, 2, 1, INF, INF, INF},
{6, 2, 0, 1, 4, 2, INF},
{INF, 1, 1, 0, 2, INF, 4},
{INF, INF, 4, 2, 0, 2, 1},
{INF, INF, 2, INF, 2, 0, 1},
{INF, INF, INF, 4, 1, 1, 0}
};
void floydWarshal(){
int cost[NODE][NODE]; //defind to store shortest distance from any node to any node
for(int i = 0; i<NODE; i++)
for(int j = 0; j<NODE; j++)
cost[i][j] = costMat[i][j]; //copy costMatrix to new matrix
for(int k = 0; k<NODE; k++){
for(int i = 0; i<NODE; i++)
for(int j = 0; j<NODE; j++)
if(cost[i][k]+cost[k][j] < cost[i][j])
cost[i][j] = cost[i][k]+cost[k][j];
}
cout << "The matrix:" << endl;
for(int i = 0; i<NODE; i++){
for(int j = 0; j<NODE; j++)
cout << setw(3) << cost[i][j];
cout << endl;
}
}
int main(){
floydWarshal();
}输出
The matrix: 0 3 5 4 6 7 7 3 0 2 1 3 4 4 5 2 0 1 3 2 3 4 1 1 0 2 3 3 6 3 3 2 0 2 1 7 4 2 3 2 0 1 7 4 3 3 1 1 0
更新于: 2023年11月7日
70K+ 浏览量
广告