数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究单源最短路径，非负权重
单源最短路径算法（对于非负权重）也称为 Dijkstra 算法。给定一个图 G(V,E) 及其邻接矩阵表示，并提供一个源顶点。Dijkstra 算法用于查找从源顶点到图 G 中任何其他顶点的最小最短路径。
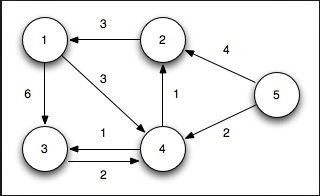
从起始节点到任何其他节点，找到最小的距离。在这个问题中，图使用邻接矩阵表示。（对于此目的，成本矩阵和邻接矩阵是相似的）。
输入 - 邻接矩阵 -
0 3 6 ∞ ∞ ∞ ∞ 3 0 2 1 ∞ ∞ ∞ 6 2 0 1 4 2 ∞ ∞ 1 1 0 2 ∞ 4 ∞ ∞ 4 2 0 2 1 ∞ ∞ 2 ∞ 2 0 1 ∞ ∞ ∞ 4 1 1 0
输出 -
0 to 1, Using: 0, Cost: 3 0 to 2, Using: 1, Cost: 5 0 to 3, Using: 1, Cost: 4 0 to 4, Using: 3, Cost: 6 0 to 5, Using: 2, Cost: 7 0 to 6, Using: 4, Cost: 7
算法
dijkstraShortestPath(n, dist, next, start)
输入 - 节点总数 n，每个顶点的距离列表，存储下一个节点的 next 列表，以及种子或起始顶点。
输出 - 从起始节点到所有其他顶点的最短路径。
Begin create a status list to hold the current status of the selected node for all vertices u in V do status[u] := unconsidered dist[u] := distance from source using cost matrix next[u] := start done status[start] := considered, dist[start] := 0 and next[start] := φ while take unconsidered vertex u as distance is minimum do status[u] := considered for all vertex v in V do if status[v] = unconsidered then if dist[v] > dist[u] + cost[u,v] then dist[v] := dist[u] + cost[u,v] next[v] := u done done End
示例（C++）
#include<iostream>
#define V 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[V][V] = {
{0, 3, 6, INF, INF, INF, INF},
{3, 0, 2, 1, INF, INF, INF},
{6, 2, 0, 1, 4, 2, INF},
{INF, 1, 1, 0, 2, INF, 4},
{INF, INF, 4, 2, 0, 2, 1},
{INF, INF, 2, INF, 2, 0, 1},
{INF, INF, INF, 4, 1, 1, 0}
};
int minimum(int *status, int *dis, int n){
int i, min, index;
min = INF;
for(i = 0; i<n; i++)
if(dis[i] < min && status[i] == 1){
min = dis[i];
index = i;
}
if(status[index] == 1)
return index;//minimum unconsidered vertex distance
else
return -1;//when all vertices considered
}
void dijkstra(int n, int *dist,int *next, int s){
int status[V];
int u, v;
//initialization
for(u = 0; u<n; u++){
status[u] = 1;//unconsidered vertex
dist[u] = costMat[u][s];//distance from source
next[u] = s;
}
//for source vertex
status[s] = 2; dist[s] = 0; next[s] = -1;//-1 for starting vertex
while((u = minimum(status, dist, n)) > -1){
status[u] = 2;//now considered
for(v = 0; v<n; v++)
if(status[v] == 1)
if(dist[v] > dist[u] + costMat[u][v]){
dist[v] = dist[u] + costMat[u][v];//update distance
next[v] = u;
}
}
}
main(){
int dis[V], next[V], i, start = 0;
dijkstra(V, dis, next, start);
for(i = 0; i<V; i++)
if(i != start)
cout << start << " to " << i <<", Using: " << next[i] << ", Cost: " << dis[i] << endl;
}输出
0 to 1, Using: 0, Cost: 3 0 to 2, Using: 1, Cost: 5 0 to 3, Using: 1, Cost: 4 0 to 4, Using: 3, Cost: 6 0 to 5, Using: 2, Cost: 7 0 to 6, Using: 4, Cost: 7
更新于: 2020-07-02
725 次查看
广告