有向加权图中从源到目的地的单调最短路径

---

寻路算法基于图搜索技术，研究节点之间的路径，从一个节点开始，通过连接逐步前进，直到达到目标。在这篇文章中，我们将讨论加权图以及如何在有向加权图中计算从源节点到目标节点的单调最短路径。

什么是加权图？

加权图将图与权重函数结合起来。也就是说，它为每条边分配一个整数权重。

图的边权重有多种用途：

• 网络连接延迟

• 道路网络距离

• 社交网络交互的强度

有两种主要计算方法来表示权重：

• 在邻接表中，为每个顶点注册边权重。

• 维护一个单独的集合数据结构，将每条边映射到其权重。

单调最短路径

如果路径上每条边的权重都严格递增或严格递减，则该路径是单调的。

最短路径的属性是什么？

最短路径的属性如下：

• 权重并不总是距离。几何直觉很有帮助，但边权重表示时间或成本。

• 最短路径总是最简单的。

• 负权重使事情变得复杂。目前，我们假设边权重为正（或零）。

• 路径是定义好的。最短路径必须保持边的方向。

• 并非所有顶点都必须可访问。如果一个节点无法从另一个节点访问，则不存在路径。因此，从 s 到 t 不存在最短路径。

• 在单个顶点或节点与其他节点之间，可能存在多条具有最小权重的路径。

• 可以存在平行边和自环。

迪杰斯特拉最短路径算法

此方法首先确定起始节点与所有直接连接节点之间最低权重的关系。它跟踪每个权重并转到“最接近”的节点。然后它重复计算，但这次是从原始节点开始的累积和。此过程保持这种方式，评估所有增量权重，并且始终采用到目标节点的权重最小的累积路径。

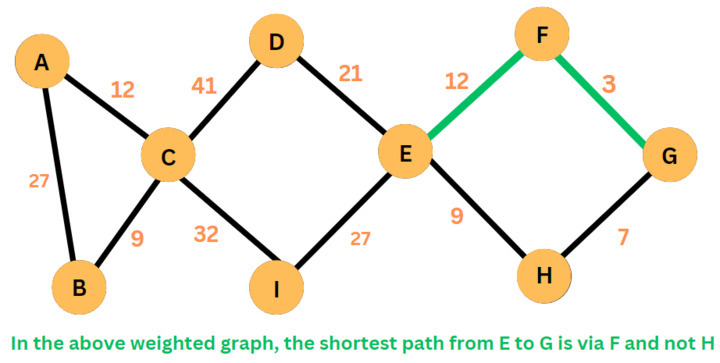
所有节点对最短路径 (APSP) 算法

这将找到连接任意两个节点的最小距离路径。它比对网络的每两个顶点实现 SSSP 方法更快。

APSP 通过维护已确定权重的计数来改进流程，从而同时执行多个顶点。这些确定的权重用于查找未知顶点的最短路径。

何时可以使用所有节点对最短路径？

当最短路径受阻或次优时，通常使用“所有节点对最短路径”来探索替代方向。例如，此方法确保逻辑路由规划中多样化路由的最佳多条路径。在评估所有节点之间所有或大多数替代路径时，使用 APSP。

单源最短路径 (SSSP)

“SSSP 算法”在主节点和网络中的每个节点之间找到“最短加权路径”。

它是如何工作的？

它按此顺序工作：

这一切都从根节点开始，从中评估每条路径。

选择与根节点之间权重最小的链接并将其合并到树中，以及其关联的节点。

以类似的方式选择从根节点到每个未访问节点的下一个具有最小累积权重的关系，并将其放入树中。

一旦没有更多节点可以放置，则过程完成，并且获得 SSSP。

何时可以使用此算法？

当需要确定从已识别的初始位置到所有其他节点的最佳路径时，使用 SSSP 算法。由于路径由从根开始的总路径权重确定，因此它有利于确定到每个节点的最佳路径，但在必须一次访问所有节点时并不总是必要。

有向加权图中从源到目的地的单调最短路径

按照以下说明解决问题：

对递增和递减路径分别运行两次迪杰斯特拉算法。

• 使用“迪杰斯特拉算法求递减最短路径”更新从一个节点到另一个节点的最短路径，如果节点之间的边权重小于朝向源节点的最小距离路径的边权重。

• 对于递增最短路径也是如此：仅当边长于朝向源节点的最小距离路径的边时，才更新从一个节点到另一个节点的最短路径。

如果尚未到达目标顶点，则不存在合法最短路径。

如果递增和递减最短路径的两次迪杰斯特拉算法传递均未提供可行的路径，则返回 -1。

示例

#include <bits/stdc++.h>
#include <limits>
#include <queue>
#include <vector>
 
using namespace std;

// Represents a vertex in the graph
class Vertex {
   public:
      int id;
      vector<int> adj_list;
      vector<double> adj_weights;
 
   // A constructor which accepts the id of the vertex
   Vertex(int num)
   : id(num){
   }
};
 
// Finds the monotonic shortest path using Dijkstra's algorithm
double shortest_path(vector<Vertex>& vertices, int src, int destination){
   int N = vertices.size() - 1;
 
   // Stores distance from src and edge on the shortest path from src
   vector<double> distTo(N + 1, numeric_limits<double>::max());
   vector<double> edgeTo(N + 1, numeric_limits<double>::max());
 
   // Setting initial distance from src to the highest value
   for (int i = 1; i <= N; i++) {
      distTo[i] = numeric_limits<double>::max();
   }
 
   // Monotonic decreasing pass of Dijkstra's
   distTo[src] = 0.0;
   edgeTo[src] = numeric_limits<double>::max();
 
   priority_queue<pair<double, int>,
   vector<pair<double, int> >,
   greater<pair<double, int> > >
   pq;
   pq.push(make_pair(0.0, src));
 
   while (!pq.empty()) {
      // Take the vertex with the closest current distance from src
      pair<double, int> top = pq.top();
      pq.pop();
      int closest = top.second;
 
      for (int i = 0; i < vertices[closest].adj_list.size(); i++) {
         int neighbor = vertices[closest].adj_list[i];
         double weight = vertices[closest].adj_weights[i];
 
         // Checks if the edges are decreasing and whether the current directed edge will create a shorter path
         if (weight < edgeTo[closest] && distTo[closest] + weight < distTo[neighbor]) {
            edgeTo[neighbor] = weight;
            distTo[neighbor] = distTo[closest] + weight;
            pq.push(make_pair(distTo[neighbor], neighbor));
         }
      }
   }
 
   // Store the result of the first pass of Dijkstra's
   double first_pass = distTo[destination];
 
   // Monotonic increasing pass of Dijkstra's
   for (int i = 1; i <= N; i++) {
      distTo[i] = numeric_limits<double>::max();
   }
 
   distTo[src] = 0.0;
   edgeTo[src] = 0.0;
 
   pq.push(make_pair(0.0, src));
 
   while (!pq.empty()) {
      // Take the vertex with the closest current distance from src
      pair<double, int> top = pq.top();
      pq.pop();
      int closest = top.second;
 
      for (int i = 0; i < vertices[closest].adj_list.size(); i++) {
         int neighbor = vertices[closest].adj_list[i];
         double weight = vertices[closest].adj_weights[i];
 
         // Checks if the edges are increasing and whether the current directed edge will create a shorter path
         if (weight > edgeTo[closest] && distTo[closest] + weight < distTo[neighbor]) {
            edgeTo[neighbor] = weight;
            distTo[neighbor] = distTo[closest] + weight;
            pq.push(make_pair(distTo[neighbor], neighbor));
         }
      }
   }
 
   // Store the result of the second pass of Dijkstras
   double second_pass = distTo[destination];
 
   if (first_pass == DBL_MAX && second_pass == DBL_MAX)
      return -1;
 
   return min(first_pass, second_pass);
}
 
// Driver Code
int main(){
   int N = 6, M = 9, src, target;
 
   // Create N vertices, numbered 1 to N
   vector<Vertex> vertices(N + 1, Vertex(0));
 
   for (int i = 1; i <= N; i++) {
      vertices[i] = Vertex(i);
   }
 
   // Add M edges to the graph
   vertices[1].adj_list.push_back(3);
   vertices[1].adj_weights.push_back(1.1);
 
   vertices[1].adj_list.push_back(5);
   vertices[1].adj_weights.push_back(2.0);
 
   vertices[1].adj_list.push_back(6);
   vertices[1].adj_weights.push_back(3.3);
 
   vertices[2].adj_list.push_back(5);
   vertices[2].adj_weights.push_back(2.7);
 
   vertices[3].adj_list.push_back(4);
   vertices[3].adj_weights.push_back(2.0);
 
   vertices[3].adj_list.push_back(5);
   vertices[3].adj_weights.push_back(1.1);
 
   vertices[4].adj_list.push_back(2);
   vertices[4].adj_weights.push_back(2.3);
 
   vertices[5].adj_list.push_back(6);
   vertices[5].adj_weights.push_back(2.4);
 
   vertices[6].adj_list.push_back(2);
   vertices[6].adj_weights.push_back(3.0);
 
   // src and destination vertices
   src = 1;
   target = 2;
   double shortest = shortest_path(vertices, src, target);
   cout << shortest << endl;
   return 0;
}

输出

根据以上代码：

5.4

在加权图中查找最短路径的替代方法

“贝尔曼-福特算法”表示一种“单源最短路径”技术。这意味着，给定一个加权网络，此方法将提供任意两个顶点之间的最小距离路径。

与迪杰斯特拉算法相比，贝尔曼-福特算法可以在具有负权重边的图上运行。因此，贝尔曼-福特算法更受许多人的青睐。

此算法的示例包括动态规划。它从单个节点开始，然后评估可以使用一条边访问的更多顶点之间的距离。然后它继续搜索包含两条边的路径，并且该过程继续进行。贝尔曼-福特算法采用自底向上的策略。

结论

寻路算法可以帮助我们理解数据之间的联系。运行两次迪杰斯特拉算法可以找到源节点和目标节点之间的最小距离路径。此方法使用边权重来查找一条路径，该路径减少了源节点和所有其他节点之间的累积权重。