平面图及其性质

如果一个图 'G' 可以绘制在平面上或球面上，并且没有任何两条边在非顶点处相交，则称该图 'G' 为平面图。

示例

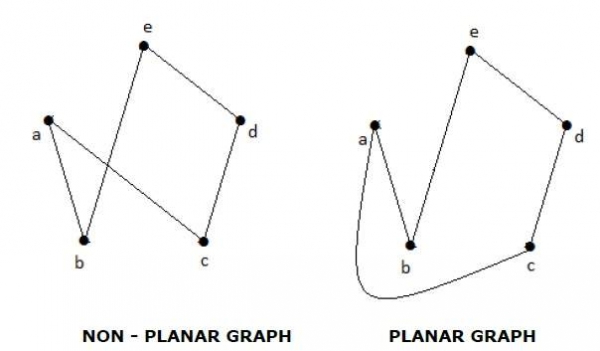
区域

每个平面图将平面划分为称为区域的连通区域。

示例

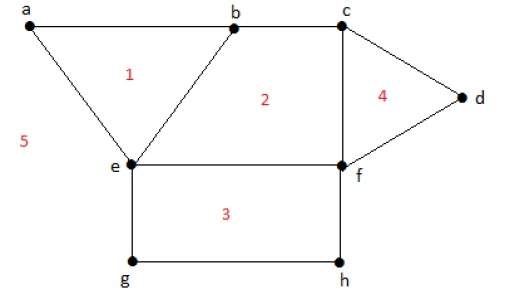
有界区域的度数 r = deg(r) = 包围区域 r 的边的数量。

deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8

无界区域的度数 r = deg(r) = 包围区域 r 的边的数量。

deg(R1) = 4
deg(R2) = 6

在平面图中，以下性质成立：

  • 1. 在具有 'n' 个顶点的平面图中，所有顶点的度数之和为

    n ∑ i=1 deg(Vi) = 2|E|

  • 2. 根据区域度数之和定理，在具有 'n' 个区域的平面图中，区域度数之和为：

    n ∑ i=1 deg(ri) = 2|E|

基于上述定理，您可以得出以下结论：

在平面图中，

  • 如果每个区域的度数为 K，则区域度数之和为

    K|R| = 2|E|

  • 如果每个区域的度数至少为 K(≥ K)，则

    K|R| ≤ 2|E|

  • 如果每个区域的度数至多为 K(≤ K)，则

    K|R| ≥ 2|E|

注意 - 假设所有区域具有相同的度数。

3. 根据平面图上的欧拉公式，

  • 如果图 'G' 是连通平面图，则

    |V| + |R| = |E| + 2

  • 如果平面图具有 'K' 个连通分量，则

    |V| + |R|=|E| + (K+1)

其中，|V| 是顶点数，|E| 是边数，|R| 是区域数。

4. 边顶点不等式

如果 'G' 是一个连通平面图，每个区域的度数至少为 'K'，则

|E| ≤ k/k - 2{|v|-2}

您知道，|V| + |R| = |E| + 2

       K.|R| ≤ 2|E|

      K(|E| - |V| + 2) ≤ 2|E|

      (K - 2)|E| ≤ K(|V| - 2)

      |E| ≤ k/k - 2{|v| - 2}

5. 如果 'G' 是一个简单连通平面图，则

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

存在至少一个顶点 V ∈ G，使得 deg(V) ≤ 5

6. 如果 'G' 是一个简单连通平面图（至少有 2 条边）且没有三角形，则

|E| ≤ {2|V| – 4}

7. 库拉托夫斯基定理

图 'G' 为非平面图当且仅当 'G' 具有一个同胚于 K5 或 K3,3 的子图。

更新于： 2019年8月23日

5K+ 浏览量

开启您的 职业生涯

通过完成课程获得认证

开始学习
广告