图及其遍历算法

在本节中，我们将了解图数据结构以及其遍历算法。

图是一种非线性数据结构，由一些节点及其连接的边组成。边可以是有向的或无向的。该图可以表示为 G(V, E)。以下图可以表示为 G({A, B, C, D, E}, {(A, B), (B, D), (D, E), (B, C), (C, A)})

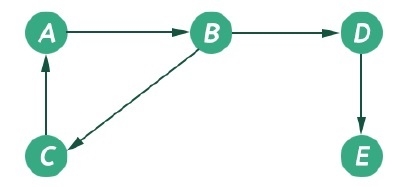
图具有两种类型的遍历算法。它们被称为广度优先搜索和深度优先搜索。

广度优先搜索 (BFS)

广度优先搜索 (BFS) 遍历是一种用于访问给定图的所有节点的算法。在这个遍历算法中，选择一个节点，然后逐个访问所有相邻节点。在完成所有相邻顶点后，它会继续检查另一个顶点并再次检查其相邻顶点。

算法

bfs(vertices, start)
Input: The list of vertices, and the start vertex.
Output: Traverse all of the nodes, if the graph is connected.
Begin
   define an empty queue que
   at first mark all nodes status as unvisited
   add the start vertex into the que
   while que is not empty, do
      delete item from que and set to u
      display the vertex u
      for all vertices 1 adjacent with u, do
         if vertices[i] is unvisited, then
            mark vertices[i] as temporarily visited
            add v into the queue
         mark
      done
      mark u as completely visited
   done
End

深度优先搜索 (DFS)

深度优先搜索 (DFS) 是一种图遍历算法。在这个算法中，给定一个起始顶点，当找到一个相邻顶点时，它会首先移动到该相邻顶点并尝试以相同的方式进行遍历。

算法

dfs(vertices, start)
Input: The list of all vertices, and the start node.
Output: Traverse all nodes in the graph.
Begin
   initially make the state to unvisited for all nodes
   push start into the stack
   while stack is not empty, do
      pop element from stack and set to u
      display the node u
      if u is not visited, then
         mark u as visited
         for all nodes i connected to u, do
            if ith vertex is unvisited, then
               push ith vertex into the stack
               mark ith vertex as visited
         done
   done
End

Arnab Chakraborty

更新于：2023年9月8日

46K+ 次浏览

启动您的职业生涯

完成课程获得认证

开始学习