线性图的应用

---

引言

线性图的应用在日常生活中随处可见。形如直线Ax+By+C=0的图称为线性图。在标准的直线方程中，A和B是系数，x和y是变量，C是常数。

简单来说，线性图表示两个或多个变量之间的关系。通过将方程的变量（例如x、y、z等点）绘制在图上，我们得到一条直线。线性图的应用广泛应用于分析和预测各个科学领域中的未来事件。

在本教程中，我们将学习线性图及其应用，并附带一些已解决的问题。

线性图

表示两个或多个变量之间关联的图表或图形称为线性图。变量也可以被视为数量。

它们用于显示一段时间内一系列数据点的变化。

例如：

下表给出了X先生2000年至2005年的年收入。

年份	2000	2001	2002	2003	2004
年收入（百万）	1.5	2.5	3.6	5	6.5

线性图的应用

• 线性图用于根据时间查找运动物体的位移、速度、速度、距离等。

• 线性图还可以表示一段时间内的资金和支出或收入。

• 在制药研究中，通过应用线性图可以找到药物的精确效力。

• 可以借助线性图绘制一个人根据身高估算体重的图表。

• 可以通过线性图读取特定研究中观察到的人或地方的一组摄氏度转换为华氏度的值。

• 该图还可以显示一段时间内特定国家的人口数量。

• 可以通过线性图研究一段时间内自然资源的消耗情况。

已解决的例子

1)对于给定方程2x-y=2，提供一组x值x=2,4,6,8和10，求相应的y值，并在线性图中表示这些值。

答案

将x值代入给定方程2x-y=2，我们得到

$$\mathrm{2(2)-y=2}$$

$$\mathrm{4-y-2=0}$$

$$\mathrm{\Rightarrow y= 2}$$

$$\mathrm{2(4)-y=2}$$

$$\mathrm{8-y-2=0}$$

$$\mathrm{\Rightarrow y= 6}$$

$$\mathrm{2(6)-y=2}$$

$$\mathrm{12-y-2=0}$$

$$\mathrm{\Rightarrow y= 10}$$

$$\mathrm{2(8)-y=2}$$

$$\mathrm{16-y-2=0}$$

$$\mathrm{\Rightarrow y= 14}$$

$$\mathrm{2(10)-y=2}$$

$$\mathrm{20-y-2=0}$$

$$\mathrm{\Rightarrow y= 18}$$

将x和y值制成表格，我们得到

x	2	4	6	8	10
y	2	6	10	14	18

通过绘制上述点，我们得到一个线性图

2)将给定点绘制在图上，

x	1	2	3	4	5
y	0	4	7	10	13

答案

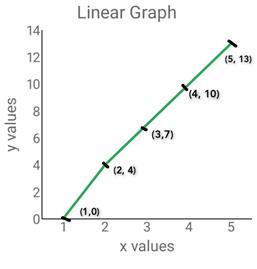
因此，上图显示了给定的x和y值。

3)根据下图的线性图，将x和y值制成表格。

答案

当对上图中给出的x和y值制表时，我们得到

x	1.5	2.2	3.5	4.5
y	2	4.3	8.1	10

4)弗雷德开车4.8小时行驶11.9公里到达目的地。让我们阅读他的游记以了解更多详情。

当弗雷德开始驾车时，他行驶2.5小时后第一次休息。到那时，他已经行驶了4.4公里。然后他以3小时行驶6.2公里，3.5小时行驶8公里，3.8小时行驶8.5公里，最后以11.9公里到达目的地。将给定数据表示为图形。所得图形是线性的吗？

答案

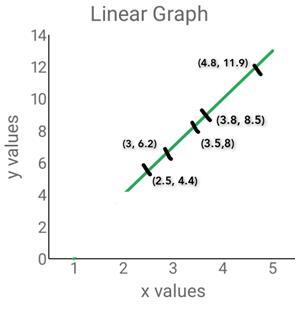
因此，我们以图形方式表示了给定数据。是的，所得图形是线性的。

5)X公司产量增长率如下所示。

根据给定的线性图，找出以下内容

• 哪一年产品的生产率提高到3.6？

• (b) 2003年X公司的产品生产率是多少？

答案

• 从给定的线性图可以看出，2002年产品的生产率提高到3.6。

• 2003年X公司的产品生产率为5。

结论

• 直线的通式为Ax+By+C=0。

• 次数为一的方程称为线性方程。

• 如果图上绘制的点形成一条直线，则称其为线性。

• 如果次数为一的方程表示为图或直线，则称其为线性。

• 线性图表示两个或多个变量之间的关系。

常见问题

1. 如果线性方程写成y = mx +b的形式怎么办？

如果线性方程的形式为y = mx + b，则称为直线的斜率或y截距。此形式也称为斜率截距式或斜率截距方程。此外，它被称为直线的通式。

2. 线性方程中的有序对是什么？

有序对以(x,y)的形式表示。它包含绘制的或获得的x和y坐标。它被称为给定线性方程组的解。

3. 我们如何判断给定的线性方程组是否一致？

在图中，如果我们发现给定线性方程组的绘制值形成任何交点或重合，则给定的线性方程对是一致的。

4. 一致线性方程组的唯一解和无限解之间有什么区别？

在图中，如果我们发现方程的值有一个交点，则解是唯一的。

同样，在图中，如果方程的值只形成一个重合点，则可以肯定的是，给定的一致线性方程对有无限多个解。

5. 解线性方程的图形表示法是什么？

用消元法解出的给定线性方程组的值的图形表示也可以称为解线性方程的图形法。

如果我们绘制第一个方程的图形，然后绘制后续方程，则直线将在四个象限之一的点(x,y)处相交。该点将是通过代入法或交叉相乘法获得的精确解。

6. 线性图和线图有什么区别？

• 连接以形成线性图的点集是共线的。

• 连接以形成线图的点集可能不是共线的。