线性规划

---

简介

线性规划或线性优化是一种独特的工具，用于获得数学模型的最优（最大或最小）值。它缩写为 LP，也称为数学优化。在本教程中，我们将学习线性规划、解决线性规划问题的不同方法及其各种类型。

线性规划

• 线性规划被定义为数学优化过程，其中在特定约束条件下评估过程结果的最大值和最小值。

• 换句话说，它是一种优化线性目标函数的技术。

• 线性规划问题 (LPP) 包括三个部分：目标函数、线性等式或约束以及非负限制。

• 目标函数是过程变量的线性函数，需要对其进行优化。

• 约束是过程变量的边界限制或限制。线性规划问题的标准形式可以表示为

目标函数 − $\mathrm{g(x_{1},x_{2}\:=\:q_{1}x_{1}\:+\:q_{2}x_{2})}$

约束 − $\mathrm{m_{11}x_{1}\:m_{12}x_{2}\:\leq\:s_{1}}$

$\mathrm{m_{21}x_{1}\:+\:m_{22}x_{2}\:\leq\:s_{2}}$

非负限制 − $\mathrm{x_{1}\:\geq\:0,\:x_{2}\:\geq\:0}$

解决 LPP 的方法

主要有两种方法可以解决 LPP，例如

• 图解法

• 单纯形法

让我们详细讨论每种方法。

图解法

• 将 LPP 构造为标准形式。

• 在笛卡尔平面上绘制图形并绘制约束线

• 确定每条约束线的有效侧。

• 评估可行解区域并获得角点

• 将角点代入目标函数以获得所需结果

单纯形法

• 步骤 1 − 第一步涉及将松弛变量添加到目标函数中，以将不等式转换为方程形式。

• 步骤 2 − 构造初始单纯形表并将目标函数写为底行。

• 步骤 3 − 识别列中最负的条目并标记为枢轴列。

• 步骤 4 − 通过将最右列中的条目除以枢轴列中的条目来找到商。包含最小商的行标记为枢轴行。标记枢轴元素，即枢轴行和列的交点

• 步骤 5 − 通过执行基本运算使枢轴列的所有条目都变为零。

• 步骤 6 − 如果我们在底行得到非负整数，则停止此步骤；否则，从步骤 4 开始重复此步骤。

LPP 的类型

以下是下面讨论的 LPP 类型。

营养

这种类型的 LPP 用于优化膳食计划。换句话说，以最低预算优化食物摄入量是此 LPP 的目标。

• 目标函数 − 膳食预算

• 约束 − 食品中特定膳食的最低/最高量，例如糖和胆固醇。

生产/成本

这种类型的 LPP 涉及优化制造单位的净利润或生产率。

• 目标函数 − 生产率或净利润

• 约束 − 生产成本、员工成本、包装成本等。

运输

此 LPP 旨在以最低成本提供高效的运输

• 目标函数 − 运输成本

• 约束 − 商品的供应或需求

解题示例

示例 1

一种面包需要 250 克面粉和 20 克脂肪。另一种面包需要 150 克面粉和 30 克脂肪。求从 3 公斤面粉和 0.6 公斤脂肪中可以生产的最大面包数量。

解决方案 −

步骤 1 − 让我们将给定数据制成表格以便更好地理解

	面粉重量（克）	脂肪重量（克）
第一种面包 (x)	250	20
第二种面包 (y)	150	30
可用量	3000	600

步骤 2 − 我们必须根据给定数据制定目标函数和约束条件。

目标函数 $\mathrm{g\:=\:x\:+\:y}$

约束 $\mathrm{250x\:+\:150y\:\leq\:3000\:or\:5x\:+\:3y\:\leq\:60}$

$\mathrm{20x\:+\:30y\:\leq\:600\:or\:2x\:+\:3y\:\:leq\:60}$

非负限制 $\mathrm{x_{1}\:\geq\:0\:,\:x_{2}\:\geq\:0}$

步骤 3 − 在笛卡尔平面上绘制直线，即 $\mathrm{5x\:+\:3y\:=\:60}$ 和 $\mathrm{2x\:+\:3y\:=\:60}$。

约束线 $\mathrm{5x\:+\:3y\:=\:60}$ 与坐标轴在 (12, 0) 和 (0, 20) 处相交。因此，位于直线区域下方的任何点都满足 $\mathrm{5x\:+\:3y\:\leq\:60}$

同样，线 $\mathrm{2x\:+\:3y\:=\:60}$ 与坐标轴在 (30, 0) 和 (0, 20) 处相交。因此，位于直线区域下方的任何点都满足 $\mathrm{2x\:+\:3y\:\leq\:60}$。角点和目标函数的相应值如下所示

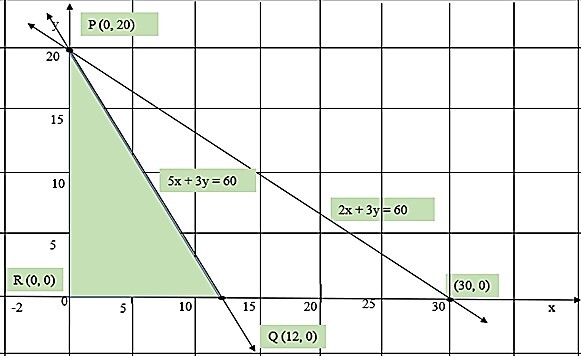
角点	$\mathrm{g(x,y)\:=\:x\:+\:y}$
P (0, 20)	20
Q (12. 0)	12
R (0,0)	0

∴可以形成的最大面包数量为 20，最优解为 (0,20)。

示例 2

使用单纯形法求解 LPP。

最大化 $\mathrm{f(x,y)\:=\:7x\:+\:5y}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:x\:+\:2y\:\leq\:6}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:4x\:+\:3y\:\leq\:12}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:x,y\:\geq\:0}$

解决方案

将松弛变量添加到上述不等式中，将其转换为方程

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:7x\:+\:5y\:=\:p}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:x\:+\:2y\:+\:q\:=\:6}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:4x\:+\:3y\:+\:r\:=\:12}$

单纯形表如下所示。

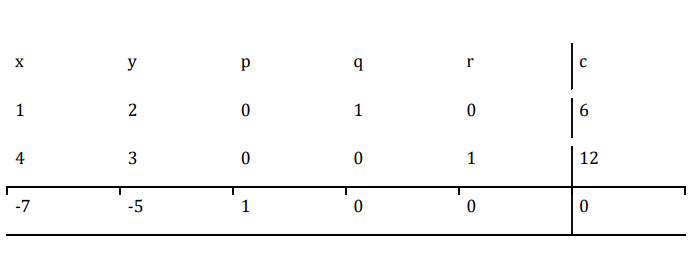
这里，第一列是枢轴列，因为它包含最大的负数 $$

现在 $\mathrm{\frac{6}{1}\:=\:6\:and\:\frac{12}{4}\:=\:3}$

由于 3 是较小的商，因此第二行是枢轴行，答案 4 是枢轴元素。

现在，使用基本运算

$\mathrm{R_{2}\:\rightarrow\:\frac{R_{2}}{4}}$

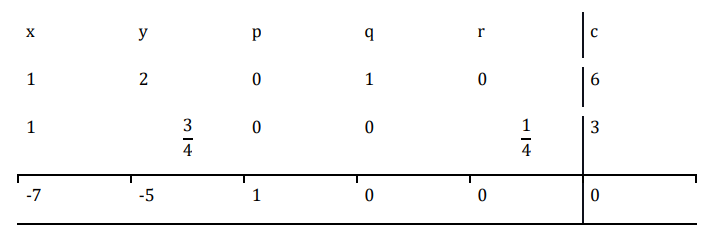
现在执行 $\mathrm{R_{1}\:\rightarrow\:R_{1}\:-\:R_{2}}$

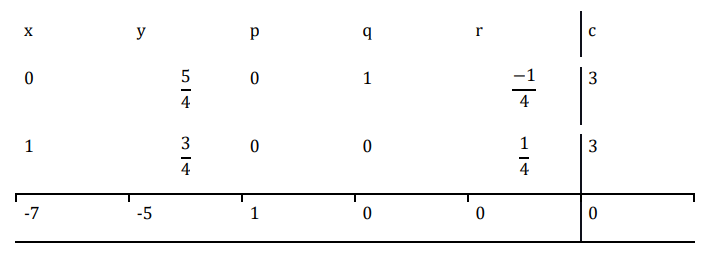
现在执行 $\mathrm{R_{3}\:\rightarrow\:7R_{2}\:+\:R_{3}}$

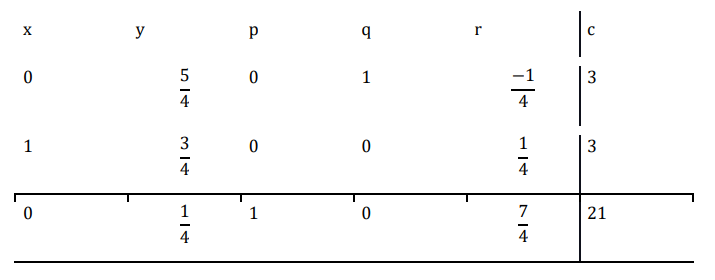
∴函数的最大值为 21，最优解为 (3,0)。

结论

本教程简要介绍了线性规划。此外，还简要描述了各种类型和解决 LPP 的方法。此外，还提供了一些解题示例，以更好地阐明这一概念。总之，它可能有助于理解线性规划问题的基本概念。

常见问题

1. 在图解法中，您所说的可行区域是什么意思？

可行区域是由满足给定约束的坐标界定的区域。

2. LP 的应用有哪些？

LP 有许多应用，包括生产调度、库存策略、技术、仓库建设等。

3. 定义目标函数？

目标函数是一个实值函数，需要对其进行最大化或最小化

4. 图解法的局限性是什么？

随着变量和约束的增加，图解法变得复杂。它更适合于随着变量和约束的增加而变得复杂的客观函数。

5. LPP 可以有多个解吗？

是的。LPP 可以有多个解。