数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中二叉树中的链表
假设我们有一个二叉树根节点和一个以头部作为第一个节点的链表。如果从头部开始的链表中的所有元素都对应于二叉树中连接的一些向下路径，则我们必须返回 True，否则返回 False。因此，如果树如下所示：
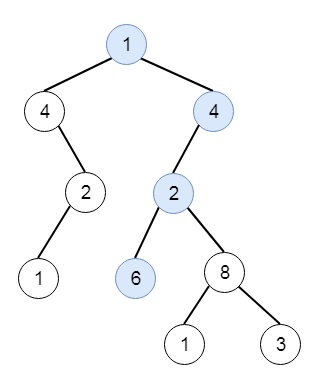
并且链表是 [1,4,2,6]，则输出将为 true。
为了解决这个问题，我们将遵循以下步骤：
定义一个映射 dp
定义一个名为 solve() 的方法，它将接收头部、根节点和标志
如果头部为空，则返回 true，或者如果根节点为空，则返回 false
如果 dp 中包含头部，并且 dp[head] 中包含根节点，并且 dp[head, root] 中包含标志，则返回 dp[head, root, flag]
如果 head 的值等于 root 的值，则
ret := solve(head 的下一个节点, root 的左子节点, false) 或 solve(head 的下一个节点, root 的右子节点, false)
如果 ret 被设置，则 dp[head, root, flag] := true 并返回 dp[head, root, flag]
dp[head, root, flag] = solve(head, root 的左子节点, flag) 或 solve(head, root 的右子节点, flag)
返回 dp[head, root, flag]
否则，当标志未设置时，返回 dp[head, root, flag] := false
否则，返回 dp[head, root, flag] := solve(head, root 的左子节点, flag) 或 solve(head, root 的右子节点, flag)
从主方法调用 solve(head, root, true)
示例 (C++)
让我们看看以下实现以更好地理解：
#include <bits/stdc++.h>
using namespace std;
class ListNode{
public:
int val;
ListNode *next;
ListNode(int data){
val = data;
next = NULL;
}
};
ListNode *make_list(vector<int> v){
ListNode *head = new ListNode(v[0]);
for(int i = 1; i<v.size(); i++){
ListNode *ptr = head;
while(ptr->next != NULL){
ptr = ptr->next;
}
ptr->next = new ListNode(v[i]);
}
return head;
}
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = right = NULL;
}
};
void insert(TreeNode **root, int val){
queue<TreeNode*> q;
q.push(*root);
while(q.size()){
TreeNode *temp = q.front();
q.pop();
if(!temp->left){
if(val != NULL)
temp->left = new TreeNode(val);
else
temp->left = new TreeNode(0);
return;
} else {
q.push(temp->left);
}
if(!temp->right){
if(val != NULL)
temp->right = new TreeNode(val);
else
temp->right = new TreeNode(0);
return;
} else {
q.push(temp->right);
}
}
}
TreeNode *make_tree(vector<int> v){
TreeNode *root = new TreeNode(v[0]);
for(int i = 1; i<v.size(); i++){
insert(&root, v[i]);
}
return root;
}
class Solution {
public:
map < ListNode*, map<TreeNode*, map <bool, bool>> > dp;
bool solve(ListNode* head, TreeNode* root, bool flag = true){
if(head == NULL) return true;
if(!root) return false;
if(dp.count(head) && dp[head].count(root) && dp[head]
[root].count(flag)) return dp[head][root][flag];
if(head->val == root->val){
bool ret = solve(head->next, root->left, false) ||
solve(head->next, root->right, false);
if(ret) return dp[head][root][flag] = true;
return dp[head][root][flag] = solve(head, root->left,
flag) || solve(head, root->right, flag);
}else if(!flag) return dp[head][root][flag] = false;
else
return dp[head][root][flag]= solve(head, root->left,
flag) || solve(head, root->right, flag);
}
bool isSubPath(ListNode* head, TreeNode* root) {
return solve(head, root);
}
};
main(){
vector<int> v = {1,4,2,6};
vector<int> v1 = {1,4,4,NULL,2,2,NULL,1,NULL,6,8,NULL,NULL,NULL,NULL,1,3};
ListNode *head = make_list(v);
TreeNode *root = make_tree(v1);
Solution ob;
cout << (ob.isSubPath(head, root));
}输入
[1,4,2,6] [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出
1
2K+ 次查看
