数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时装研究
法律研究从树中移除最大边数以形成 C++ 中的偶数森林
问题陈述
给定一个具有偶数个顶点的无向树，我们需要从该树中移除最大数量的边，以使所得森林的每个连通分量都具有偶数个顶点。
举例
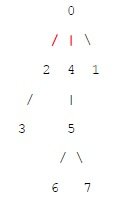
在上面所示的树中，我们可以最多移除以红色显示的 2 条边 0-2 和 0-4，以使每个连通分量都具有偶数个顶点。
算法
- 从任何起始节点进行 DFS，因为树是连接的
- 将当前节点下子树中节点的数量初始化为 0
- 对当前节点的每个子树递归执行以下操作 −
- 如果当前子树的大小为偶数，则将结果加 1，因为我们可以断开子树
- 否则将当前子树中节点的数量添加到当前计数
举例
现在，让我们看一个示例 −
#include <bits/stdc++.h>
using namespace std;
int dfs(vector<int> g[], int u, bool visit[], int& res) {
visit[u] = true;
int currComponentNode = 0;
for (int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if (!visit[v]) {
int subtreeNodeCount = dfs(g, v, visit, res);
if (subtreeNodeCount % 2 == 0)
res++;
else
currComponentNode += subtreeNodeCount;
}
}
return (currComponentNode + 1);
}
int maxEdgeRemovalToMakeForestEven(vector<int> g[], int N) {
bool visit[N + 1];
for (int i = 0; i <= N; i++)
visit[i] = false;
int res = 0;
dfs(g, 0, visit, res);
return res;
}
void addEdge(vector<int> g[], int u, int v) {
g[u].push_back(v);
g[v].push_back(u);
}
int main() {
int edges[][2] = {{0, 2}, {0, 1}, {0, 4}, {2, 3}, {4, 5}, {5, 6}, {5, 7} };
int N = sizeof(edges)/sizeof(edges[0]); vector<int> g[N + 1];
for (int i = 0; i < N; i++)
addEdge(g, edges[i][0], edges[i][1]);
cout << "Answer = " << maxEdgeRemovalToMakeForestEven(g, N) << endl;
return 0;
}输出
Answer = 2
更新于： 31-Dec-2019
339 次浏览
广告