C++ 中从完备图中获取最大可能的边不相交生成树

假设我们有一个完备图；我们需要计算边不相交生成树的数量。边不相交生成树是生成树，其中集合中的任何两棵树都没有一个共同的边。假设 N（顶点数）为 4，则输出将为 2。使用 4 个顶点的完备图如下所示 −

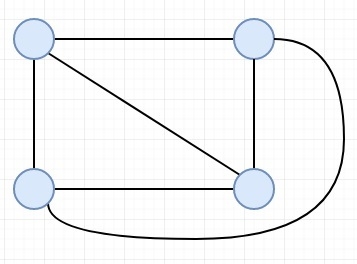
两个边不相交生成树如下 −

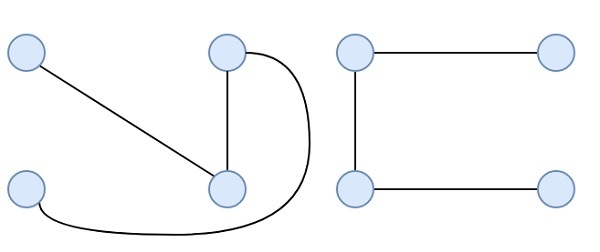
具有 N 个顶点的完备图中的边不相交生成树的最大数量为 $[\frac{n}{2}]$

范例

#include <iostream>
#include <cmath>
using namespace std;
int maxEdgeDisjointSpanningTree(int n){
   return floor(n/2);
}
int main() {
   int n = 4;
   cout << "Maximum Edge Disjoint Spanning Tree: " <<
   maxEdgeDisjointSpanningTree(n);
}

输出

Maximum Edge Disjoint Spanning Tree: 2

更新于： 21-十月-2019

182 次浏览

开启您的 职业生涯

完成课程以获得认证

开始
广告