数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学使用C++构建二叉树中两个节点能够形成的最大长度环
给定一棵二叉树，目标是找到这棵树中的最大长度环。我们将通过找到从根节点开始的左子树和右子树的最大高度，并将这些最大长度路径连接起来以获得最长环来做到这一点。
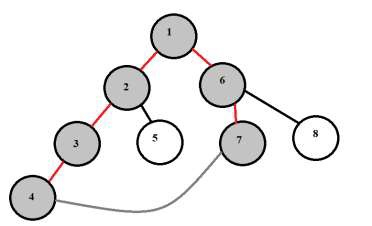
对于上面的树，最大长度环是1-2-3-4-7-6或1-6-7-4-3-2-1。长度是6。
输入 - 树
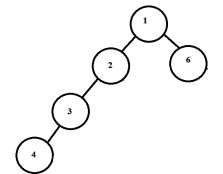
输出 - 最大长度环是 - 5
解释 - 左子树的最大高度是3，右子树的最大高度是1。环的长度变为3+1+1=5。环是1-2-3-4-6或1-6-4-3-2
输入 - 树
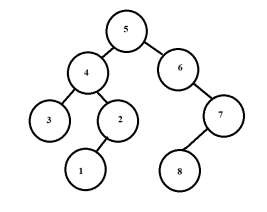
输出 - 最大长度环是 - 7
解释 - 左子树的最大高度是3，右子树的最大高度是3。环的长度变为3+3+1=7。环是5-4-2-1-8-7-6或5-6-7-8-1-2-4-5
下面程序中使用的方法如下
创建一个treenode类，它具有公共数据成员- int data表示节点的权重，left和right treenode指针指向其他此类节点。
函数newNode(int data)将数据作为参数，并创建一个左、右指针为NULL的节点。
通过调用newnode()函数创建一棵树。
函数maxheight(treenode* root)接受树的根并返回以root为根的树的最大高度。
此函数检查根是否为NULL，这意味着高度为0，返回0。
lheight和rheight分别通过递归调用maxheight(root->left);和maxheight(root->right);计算节点root的左子树和右子树的高度。
返回通过比较lheight和rheight获得的最大值。
在main函数内部，我们存储树节点的左子树和右子树的最大高度值。
现在，最大长度环是两个最大高度maxlheight + maxrheight + 1的总和，其中1是包括根节点本身。
打印环的长度作为结果。
示例
#include <bits/stdc++.h>
using namespace std;
//class for tree
class treenode{
public:
int data;
treenode* left;
treenode* right;
};
//find maximum height between left and right subtree of current root
int maxheight(treenode* root){
if (root == NULL)
return 0;
else{
int lheight = maxheight(root->left);
int rheight = maxheight(root->right);
//find maximum height
if (lheight > rheight)
return(lheight + 1);
else
return(rheight + 1);
}
}
//creating a node of tree
treenode* newNode(int data){
treenode* Node = new treenode();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return(Node);
}
int main(){
treenode *root = newNode(6);
root->left = newNode(8);
root->right = newNode(9);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->left->right->right = newNode(7);
root->left->right->right->left = newNode(2);
int maxlheight=maxheight(root->left);
int maxrheight=maxheight(root->right);
int maxlheight=maxDepth(root->left);
int maxrheight=maxDepth(root->right);
cout << "Maximum length cycle: " << maxlheight+maxrheight+1;
return 0;
}输出
Maximum length cycle: 6
更新于：2020年8月3日
194 次浏览
广告