阿伏伽德罗原子尺寸测量

---

引言

许多科学家都在尝试测量原子的尺寸。但阿伏伽德罗假说对此做出了重要的解释。阿伏伽德罗假说是在阿伏伽德罗去世两年后才被接受的。意大利化学家斯坦尼斯劳·坎尼扎罗能够解释化学中阿伏伽德罗假说的例外情况后，该假说才被接受。他解释并证明了原子、分子与各种物质重量之间的关系。

现在，我们将讨论阿伏伽德罗假说，并学习如何使用阿伏伽德罗定律计算原子的大小。

阿伏伽德罗是谁？

阿梅代奥·阿伏伽德罗，全名洛伦佐·罗马诺·阿梅代奥·卡洛·阿伏伽德罗（1776年8月9日出生，1856年7月9日去世），是一位意大利科学家。他以对气体体积(V)、压力(P)和温度(T)的研究而闻名。他推导出了被称为阿伏伽德罗定律或阿伏伽德罗假说的气体定律。对于原子理论的研究，阿伏伽德罗被认为是早期的人物，并且至今仍是重要的贡献者。

他学习教会法并自行执业。之后，阿伏伽德罗开始自学物理和数学两门学科。他和他的兄弟一起进行了第一次物理实验。

之后，他开始教学，期间他进行气体密度实验。他成为都灵大学数学物理学的第一任教授。他的主要贡献是澄清了原子和分子之间的混淆。为了纪念阿伏伽德罗，一摩尔物质中的分子数量被称为阿伏伽德罗数，也称为阿伏伽德罗常数。每摩尔克的分子实验值为$\mathrm{6.023\:\times10^{23}}$

阿伏伽德罗假说

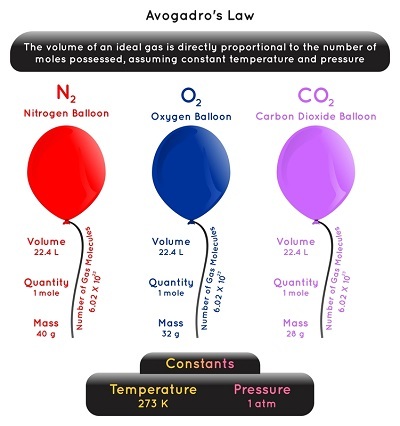
阿伏伽德罗假说也称为阿伏伽德罗原理或阿伏伽德罗定律。

它指出，在恒温恒压条件下，气体的原子或分子总数与其占据的体积成正比。

现在，如果我们取两种理想气体，并等量混合，那么它们包含相同数量的分子。如果气体（表现出理想行为）保持相同的压力和温度，这是可能的。因此，我们可以用数学公式写成：

$$\mathrm{V\:\varpropto\:n}$$

或者我们可以写成：

$$\mathrm{\frac{V}{n}\:=\:k}$$

其中，V - 气体体积

n - 气态物质，K - 特定压力和温度下的常数 在不同条件下，如果比较同一种气态物质

$$\mathrm{\frac{V_{1}}{n_{1}}\:=\frac{V_{2}}{n_{2}}}$$

因此，从上式可以看出，气体体积增加，气体摩尔数也增加。减少的情况也是如此。因此，在特定体积的气体中，存在的分子或原子总数与气体的摩尔质量无关。

阿伏伽德罗数

阿伏伽德罗数定义为：在一摩尔物质（其分子量以克为单位测量）中，单元数等于$\mathrm{6.023\:\times10^{23}}$

对于轻气体和重气体，考虑因素相同。我们讨论的单元可以是电子、离子、原子或分子，这取决于材料的性质和反应的任何倾向。

阿伏伽德罗假说如何帮助确定原子的尺寸？

利用阿伏伽德罗假说，我们可以计算出原子的半径。设物质摩尔质量为‘M’，原子数为N，

$$\mathrm{每克原子数\:=\:\frac{N}{M}}$$

$$\mathrm{每克原子的总体积\:=\:\frac{N}{M}\:\times\frac{4}{3}\:\Pi\:r^{3}}$$

根据阿伏伽德罗假说，一克物质中原子的实际体积是该克物质体积的三分之二。

$$\mathrm{\:\frac{N}{M}\:\times\frac{4}{3}\:\Pi\:r^{3}\:=\:\frac{2}{3}v}$$

{{我们知道密度，$\mathrm{\rho\:=\:\frac{质量}{体积}\:=\:\frac{1}{v}}$}}

因此，$\mathrm{\:\frac{N}{M}\:\times\frac{4}{3}\:\Pi\:r^{3}\:=\:\frac{2}{3\rho}}$

$$\mathrm{r^{3}\:=\:\frac{2\:\times\:3M}{3\rho\pi4N}\:=\:\frac{M}{2\pi\:N\rho}}$$

$$\mathrm{r\:=[\:\frac{M}{2\pi\:N\rho\:}]^{\frac{1}{3}}}$$

因此，根据这个公式，我们可以很容易地计算出原子的半径，从而计算出原子的尺寸。

例题 -

例1：飞轮中20升体积容纳10摩尔空气。但有时飞轮会损失50升体积。求飞轮漏气量。（假设温度和压力保持恒定）

解：已知，初始空气量，𝑛1 $\mathrm{n_{1}\:=\:10\:mol}$

飞轮的初始体积，$\mathrm{v_{1}\:=\:20\:L}$

飞轮的最终体积，$\mathrm{v_{2}\:=\:50\:L}$

根据阿伏伽德罗定律

$$\mathrm{\frac{v_{1}}{n_{1}}\:=\:\frac{v_{2}}{n_{2}}}$$

$$\mathrm{n_{2}\:=\:\frac{v_{2}}{v_{1}}\:\times\:n_{1}}$$

$$\mathrm{n_{2}\:=\:\frac{50}{20}\:\times\:10}$$

$$\mathrm{n_{2}\:=25\:mol}$$

因此，飞轮漏气量为25摩尔。

例2：一个气球最初充入2摩尔氢气，体积为2.5升。如果再加入2摩尔氢气，气球的体积是多少？考虑压力和温度保持恒定。

解：已知，初始气体量 $\mathrm{n_{1}\:=2\:mol}$

气球的初始体积，$\mathrm{v_{1}\:=2.5\:L}$

最终气体量，$\mathrm{n_{2}\:=2\:+\:2\:=\:4\:mol}$

根据阿伏伽德罗定律

$$\mathrm{v_{2}\:=\frac{V_{1}}{N_{1}}\:\times\:n_{2}}$$

$$\mathrm{v_{2}\:=\frac{2.5}{2}\:\times\:4\:=\:5\:升}$$

因此，气球的新体积为5升。

结论

分子一词源于摩尔一词。阿伏伽德罗定律可以确定气体量 (n) 如何与其体积 (v) 相关。发现它是一种直接关系，这表明气体体积与其存在的摩尔数成正比。这表明一摩尔中含有6.023 × 10²³个分子。

阿伏伽德罗无法确定关于双原子分子特征的假设。利用这个假设，我们可以根据在一定温度和压力下组合气体体积来推断各种气体物质的化学式和原子的尺寸。

在本教程中，我们介绍了阿伏伽德罗假说、阿伏伽德罗定律、原子尺寸的测量以及阿伏伽德罗假说的局限性。

常见问题

1. 描述6.023 × 10²³个特征粒子的术语是什么？

摩尔质量是描述6.023 × 10²³个特征粒子的术语。

2. 写出阿伏伽德罗定律的一些应用？

阿伏伽德罗定律的一些应用包括：

• 它有助于确定气体的原子性。

• 给出了分子量和蒸气密度之间的关系。

• 解释盖-吕萨克定律。

• 它有助于确定气体的分子式。

3. 如果在恒温下给定气体的体积变为原来的3倍，则压力是多少？如果‘p’是气体的初始压力？

根据玻意耳定律

$$\mathrm{P_{1}\:V_{1}\:=\:P_{2}\:V_{2}}$$

$$\mathrm{\rho\:V_{1}\:=\:P_{2}\:3V_{1}}$$

$$\mathrm{P_{2}\:=\:\frac{\rho}{3}}$$

因此，压力变为$\mathrm{\frac{\rho}{3}}$

4. 阿伏伽德罗定律的局限性是什么？

它只适用于较轻的分子（如氢气或氦气）。因为它只适用于真实气体。尽管它适用于理想气体，但这导致了该定律的局限性。

5. 气体常数的其他名称是什么？

气体常数也称为理想气体常数、普适气体常数或摩尔气体常数。