可合并优先队列和斜堆

可合并优先队列

定义

随机可合并堆（也称为可合并堆或随机可合并优先队列）被定义为一种基于优先队列的数据结构，其中底层结构也是一个堆有序二叉树。但是，对于底层二叉树的形状，没有硬性规定。

优点

• 这种方法相较于类似的数据结构，具有一系列的功能，即优势。
• 它提供了比其他数据结构更简单的方法。
• 随机可合并堆的所有操作都易于应用，并且其复杂度界限中的常数因子很小。
• 此外，也不需要维护平衡条件，并且不需要节点内的卫星信息。
• 最后，这种结构表现出良好的最坏情况时间效率。大多数情况下，每个单独操作的执行时间都是对数级的，且概率很高。

斜堆

斜堆（或自调整堆）被定义为一种以二叉树实现的堆数据结构。

斜堆之所以有优势，是因为它们能够比二叉堆更快地合并。

与二叉堆不同，斜堆没有结构约束，因此无法保证树的高度是对数级的。

只需要满足两个条件：

• 必须保持一般的堆序（根节点是最小值，子树也递归地满足此条件），但不需要平衡属性（除了最后一层，所有层都必须是满的）。
• 斜堆中的主要操作只有合并。我们可以仅通过合并来实现其他操作，如插入、提取最小值等。

示例

假设斜堆 1 为：

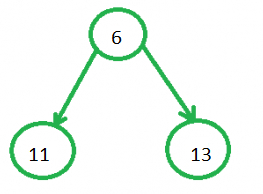
假设第二个堆为：

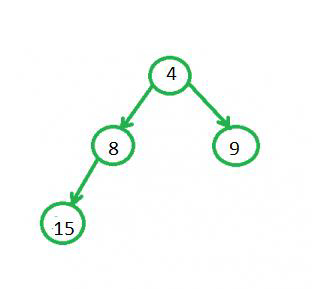
最终合并后的树形结构为：

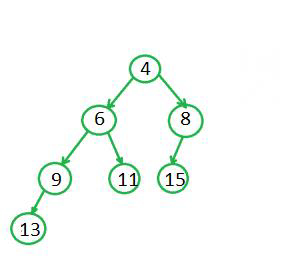
递归合并过程

merge(a1, a2)
Let a1 and a2 be the two min skew heaps to be merged. Let a1’s root be smaller than a2’s root (If not smaller, we can swap to get the same).
We swap a1->left and a1->right.
a1->left = merge(a2, a1->left)

Arnab Chakraborty

更新时间： 2020年1月2日

588 次浏览

开启你的 职业生涯

通过完成课程获得认证

立即开始