Python中的高斯-塞德尔方法建模

高斯-塞德尔方法是一种迭代方法，用于求解任何线性方程组。虽然该方法与雅可比方法非常相似，但在高斯-塞德尔方法中，在一个迭代中获得的未知数(x)的值在同一个迭代中使用，而在雅可比方法中，它们在下一个迭代级别使用。在同一步骤中更新x可以加快收敛速度。

线性方程组可以写成：

$$\mathrm{a_{1,1}x_{1} \: + \: a_{1,2}x_{2} \: + \: \dotso \: + \: a_{1,n}x_{n} \: = \: b_{1}}$$

$$\mathrm{a_{2,1}x_{1} \: + \: a_{2,2}x_{2} \: + \: \dotso \: + \: a_{2,n}x_{n} \: = \: b_{2}}$$

$$\mathrm{\vdots}$$

$$\mathrm{a_{n,1}x_{1} \: + \: a_{n,2}x_{2} \: + \: \dotso \: + \: a_{n,n}x_{n} \: = \: b_{n}}$$

因此，一般情况下，高斯-塞德尔方法可以写成：

$$\mathrm{x_{i_{new}} \: = \: − \frac{1}{a_{i,i}}(\sum_{j=1,j \neq i}^n a_{i,j}x_{j_{new}} \: − \: b_{i})}$$

其中，$\mathrm{x_{j_{new}}}$ 是在同一迭代循环中刚刚求解的方程中获得的x的新值。

高斯-塞德尔算法可以总结如下：

• 从对未知数 (x) 的一些初始猜测数组开始。

• 通过将x的猜测值代入如下所示的方程重新排列形式来计算新的x：

$$\mathrm{x_{i_{new}} \: = \: − \frac{1}{a_{i,i}}(\sum_{j=1,j \neq i}^n a_{i,j}x_{j_{new}} \: − \: b_{i})}$$

现在$\mathrm{i_{new}}$ 将是当前迭代中获得的新的x值。

• 下一步是评估新值和猜测值之间的误差，即$\mathrm{\lvert x_{new} \: − \: x_{guess} \rvert}$。如果误差大于某个收敛标准（我们将其设为$\mathrm{10^{−5}}$），则将新值赋给旧猜测值，即$\mathrm{x_{guess} \: = \: x_{new}}$，然后开始下一次迭代。

• 否则，$\mathrm{x_{new}}$ 是最终答案。

重要的是要记住，方程的对角占优性（通常称为斯卡伯勒准则）适用于高斯-塞德尔方法。如果满足以下条件，则保证高斯-塞德尔方法的收敛性：

$$\mathrm{\frac{\sum_{i\neq j \lvert a_{i,j} \rvert}}{\lvert a_{i.i} \rvert}\lbrace \substack{\le \: 1 \: 对所有方程 \\ \lt \: 1 \: 至少对一个方程}}$$

这就是为什么有时我们需要改变方程在数组中的顺序以实现所谓的对角占优的原因。

让我们通过以下示例来演示算法：

$$\mathrm{20x \: + \: y \: − \: 2z \: = \: 17}$$

$$\mathrm{3x \: + \: 20y \: − \: z \: = \: −18}$$

$$\mathrm{2x \: − \: 3y \: + \: 20z \: = \: 25}$$

将上述方程重新排列如下：

$$\mathrm{x_{new} \: = \: (−y_{guess} \: + \: 2z_{guess} \: + \: 17)/20}$$

$$\mathrm{y_{new} \: = \: (−3x_{guess} \: + \: z_{guess} \: − \: 18)/20}$$

$$\mathrm{z_{new} \: = \: (−2x_{guess} \: + \: 3y_{guess} \: + \: 25)/20}$$

现在，这些方程将在while循环中求解，以根据猜测值和当前获得的值获得未知数的新值。

模拟高斯-塞德尔方法的Python程序

实现高斯-塞德尔方法（按方程实现）的程序如下所示：

示例

# Importing modules
from pylab import *
from numpy import *

# Settingup initial guess
xg=0
yg=0
zg=0

#Error for entering in the loop
error=1

# Iteration counter
count=0

while error>1.E-5:
    count+=1

    x=(17-yg+2*zg)/20
    y=(zg-18-3*x)/20    # Here x is x_new (obtained in this step only)
    z=(25-2*x+3*y)/20   # Here x and y are x_new and y_new (obtained in this step only)

    # Evaluating and Plotting the errors
    error = abs(x-xg)+abs(y-yg)+abs(z-zg)
    figure(1,dpi=300)
    semilogy(count,error,'ko')
    xlabel('iterations')
    ylabel('error')

    # Setting the guess for the next iteration
    xg=x
    yg=y
    zg=z

savefig('error_GS.jpg')
print(f'x={round(x,5)}, y={round(y,5)}, z={round(z,5)}')

输出

程序输出将是

$$\mathrm{x \: = \: 1.0 \: , \: y \: = \: −1.0 \: , \: z \: = \: 1.0}$$

但需要注意的关键是误差图，从中可以清楚地看出，收敛解仅在五步之后就达到了。

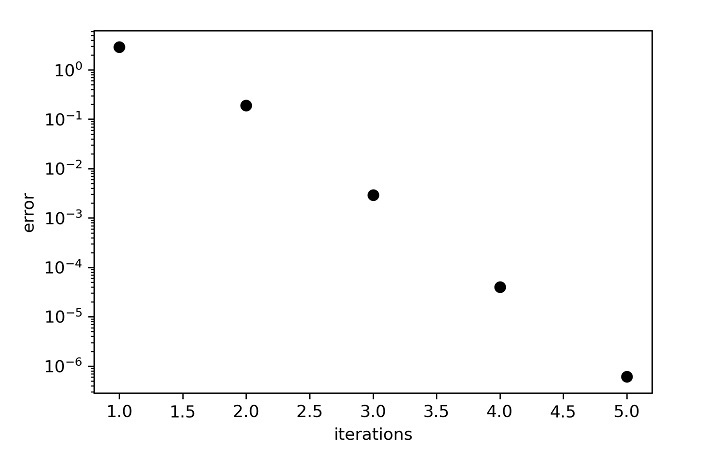
当方程的数量变大时，对我们来说，编写方程并在循环中求解就变得非常困难。因此，为了处理这个困难，系数被捆绑在一个矩阵中，可以很容易地将其插入到程序中。高斯-塞德尔实现的矩阵方法如下：

示例

# Importing modules
from pylab import *
from numpy import *

# Coefficient matrix
a=array([[20,1,-2],[3,20,-1],[2,-3,20]])
# RHS vector
b=array([17,-18,25])

# Number of rows and columns in matrix
n=len(b)

# Settingup the initial guess
xn=zeros(len(b))

# Setting error to move in loop
error=1

# Settin iteration counter
count=0

# copying guess array to new
xg=xn.copy()


while error>1.E-5:
   count+=1
   for i in range(n):
      sum1=0
      for j in range(n):
         if i!=j:
            sum1=sum1+a[i,j]*xn[j]
      xn[i]=(-1/a[i,i])*(sum1-b[i])


   # Evaluating and plotting error
   error = sum(abs(xn-xg))
   figure(1,dpi=300)
   semilogy(count,error,'ko')
   xlabel('iterations')
   ylabel('error')

   # Updating guess
   xg=xn.copy()

savefig('error_GS1.jpg')

print('x: ',xn)

输出

程序输出将是

$$\mathrm{x \: : \: 0.99999999 \: , \: −1 \: , \: 1}$$

结论

在本教程中，我们尝试对著名的Gauss-Seidel方法进行建模。已经介绍了该方法的深入算法。我们还解决了一个示例问题并给出了误差图。

高斯-塞德尔方法的成功在于方程的编写方式。如果系统是对角占优的，那么可以确保获得正确的答案，否则必须重新排列方程。

Pankaj Dumka博士

更新于：2023年10月3日

2K+ 浏览量

开启你的职业生涯

完成课程获得认证

开始学习