Python 中的割线法建模
割线法是用于求解多项式或任何超越函数的 x 截距(零点)的强大方法之一。在这种方法中,我们首先选择(基本上是猜测)我们期望根所在的区间($\mathrm{𝑥_{1}}$,$\mathrm{𝑥_{2}}$)。然后,我们绘制一条割线以连接对应于猜测值的函数上的点(A,B),如下图所示。

割线与 x 轴相交于点 $\mathrm{𝑥_{3}}$,由于 $\mathrm{𝑥_{3}}$ 和 $\mathrm{𝑥_{2}}$ 不接近(即它们的绝对差是有限的),我们找到对应于 $\mathrm{𝑥_{3}}$ 曲线上的点,即 C。然后,我们考虑点 B 和 C 连接一条割线。我们将这条线延伸到到达 X 轴,并将该点标记为 $\mathrm{𝑥_{4}}$。
现在,我们再次检查 $\mathrm{𝑥_{3}}$ 和 $\mathrm{𝑥_{4}}$ 是否接近。由于它们也不接近,因此我们找到对应于 $\mathrm{𝑥_{4}}$ 的多项式的值,并在曲线上将其标记为 D。下图表示第二条割线和点 D。
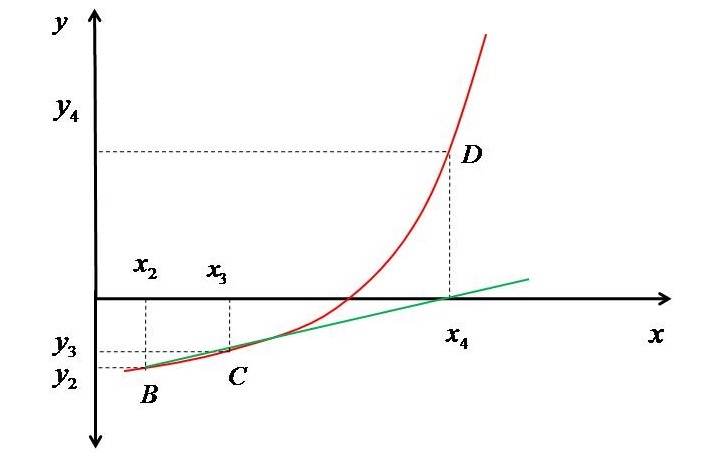
然后,我们再次在 C 和 D 之间绘制一条割线,直到“x”的下一个值和前一个值的距离收敛到一个非常小的值。因此,我们可以说该方法依次找到多项式的根,即它可以被认为是根的顺序搜索。这种方法的优点在于,x 是否位于根的一侧或围绕根并不重要。该方法通过上述解释的顺序搜索逐渐收敛到根。
现在,任务是根据前两个 x 来评估下一个 x。如果我们考虑第一条割线,那么通过它们(以评估 $\mathrm{𝑥_{3}}$)的直线方程如下:
$$\mathrm{x_{3}=x_{1}-y_{1}\frac{x_{2}-x_{1}}{y_{2}-y_{1}}}$$
而如果我们考虑第二条割线,则用于评估的直线方程如下:
$$\mathrm{x_{4}=x_{2}-y_{2}\frac{x_{3}-x_{2}}{y_{3}-y_{2}}}$$
因此,上述方程的广义版本如下:
$$\mathrm{x_{i}=x_{i-2}-y_{i-2}\frac{x_{i-1}-x_{i-2}}{y_{i-1}-y_{i-2}}}$$
Python 中的割线法实现
可以使用以下算法对割线法进行建模:
首先需要定义需要求根的函数 f(x)
选择两个任意 x 值,即 ($\mathrm{𝑥_{1}}$,$\mathrm{𝑥_{2}}$)
使用以下公式评估 x 的新值 $$\mathrm{x_{n}=x_{1}-f(x_{1})\frac{x_{2}-x_{1}}{f(x_{2})-f(x_{1})}}$$
如果 x 的新值和前一个值接近,则得到答案,即如果 $|x_{n_{}}-x2|<10^{-5}$,则 $𝑥_{𝑛}$ 是根。注意,我们取收敛准则为 $10^{-5}$,但您可以根据您的需要进行设置。
如果 $|x_{n_{}}-x2|>10^{-5}$,则设置:$𝑥_{1}$=$𝑥_{2}$ 和 $𝑥_{2}$=$𝑥_{𝑛}$
然后再次从评估新 x 的步骤开始。
然后再次从评估新 x 的步骤开始。
假设我们想要找到方程:$𝑥^{2}$+3𝑥−10=0 的根。让我们选择初始值为 ($𝑥_{1}$=−4,$𝑥_{2}$= 3)。然后执行割线法的 Python 程序如下:
# Importing module
from pylab import *
# Defining Polynomial function
def f(x):
return x ** 2 + 3 * x - 10
# Defining function for new value of x
def fn(a, b):
return a - ((b - a) / (f(b) - f(a))) * f(a)
# Creating array of x
x = linspace(-15, 15, 150)
# Plotting the function
figure(1, figsize=(7.20, 3.50))
plot(x, f(x), linewidth=2)
plot([-25, 25], [0, 0], "k--")
ylim(-15, 20)
xlim(-8, 6)
# Initial guess Interval
x1 = -4
x2 = 3
# Initial Error to enter into the loop
error = 1
# Setting iteration counter
count = 1
# Integration starts
while error > 1.E-3:
# Plotting Secant line
plot([x1, x2], [f(x1), f(x2)])
# Evaluating new value of x based on old
xn = fn(x1, x2)
# Plotting x intercept of secant
plot([xn], [0], 'o', label=f'{xn}')
# Evaluating error
error = abs(x2 - xn)
# Setting x's for next iteration
x1 = x2
x2 = xn
# Incrementing loop counter
count += 1
# Printing selected value of xn in the legend
if count < 6:
legend()
# Showing root in the figure (just decoration)
text(-7, -10, f'Root = {round(xn, 3)}', bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10})
print(f'Root = {round(xn, 3)}')
show()
上述代码清楚地说明了本节开头提到的所有步骤。上述程序的输出将如以下图所示。
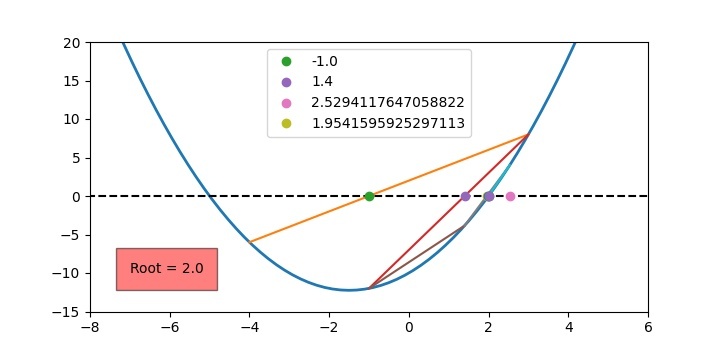
对于其他根,您可以将初始“x”取为:−6 和 −2。然后结果如下所示

结论
本文详细讨论了割线法。给出了数学背景,以便轻松地对该方法进行建模。用户可以修改上面给出的代码,并使用它来查找其他函数的根。


 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP