数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究正割法求解非线性方程\n
正割法也可用于求解非线性方程。此方法类似于牛顿-拉夫逊法，但在此处我们不需要找出函数的导数 f(x)。仅使用 f(x)，我们可以通过使用牛顿差分公式来按数值找出 f’(x)。从牛顿-拉夫逊公式我们知道，
我们知道，
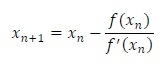
现在，使用差分公式，我们得到，
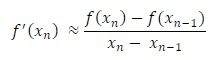
通过用新的 f’(x) 替换牛顿-拉夫逊公式中的 f’(x)，我们可以找出正割公式来求解非线性方程。
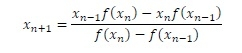
注意：对于此方法，我们需要任意两个初始猜测来开始找出非线性方程的根。
输入和输出
Input: The function f(x) = (x*x) - (4*x) - 10 Output: The root is: -1.74166
算法
secant(x1, x2)
输入：两个初始猜测为根。
输出：非线性方程 f(x) 中的近似根。
Begin f1 := f(x1) f2 := f(x2) x3 := ((f2*x1) – (f1*x2)) / (f2 – f1) while relative error of x3 and x2 are > precision, do x1 := x2 f1 := f2 x2 := x3 f2 := f(x2) x3 := ((f2*x1) – (f1*x2)) / (f2 – f1) done root := x3 return root End
示例
#include<iostream>
#include<cmath>
using namespace std;
double absolute(double value) { //to find magnitude of value
if(value < 0)
return (-value);
return value;
}
double f(double x) { //the given function x^2-4x-10
return ((x*x)-(4*x)-10);
}
double secant(double x1, double x2) {
double x3, root;
double f1, f2;
f1 = f(x1);
f2 = f(x2);
x3 = (f2*x1-f1*x2)/(f2-f1);
while(absolute((x3-x2)/x3) > 0.00001) { //test accuracy of x3
x1 = x2; //shift x values
f1 = f2;
x2 = x3;
f2 = f(x2); //find new x2
x3 = (f2*x1-f1*x2)/(f2-f1); //calculate x3
}
root = x3;
return root; //root of the equation
}
main() {
double a, b, res;
a = 0.5;
b = 0.75;
res = secant(a, b);
cout << "The root is: " << res;
}输
The root is: -1.74166
更新时间： 2020年6月17日
1K+ 浏览次数
广告