
NLP - 词级别分析
本章我们将了解自然语言处理中的词级别分析。
正则表达式
正则表达式 (RE) 是一种用于指定文本搜索字符串的语言。RE 帮助我们使用包含在模式中的特殊语法来匹配或查找其他字符串或字符串集。正则表达式在 UNIX 和 MS WORD 中以相同的方式用于搜索文本。许多搜索引擎都使用许多 RE 功能。
正则表达式的属性
以下是 RE 的一些重要属性:
美国数学家斯蒂芬·科尔·克莱尼(Stephen Cole Kleene)将正则表达式语言形式化。
RE 是用特殊语言编写的公式,可用于指定简单的字符串类,即符号序列。换句话说,我们可以说 RE 是表征字符串集的代数符号。
正则表达式需要两样东西,一个是我们要搜索的模式,另一个是我们需要从中搜索的文本语料库。
数学上,正则表达式可以定义如下:
ε 是一个正则表达式,表示该语言包含空字符串。
φ 是一个正则表达式,表示它是空语言。
如果X 和Y 是正则表达式,则
X,Y
X.Y(XY 的串联)
X+Y(X 和 Y 的并集)
X*,Y*(X 和 Y 的 Kleene 闭包)
也是正则表达式。
如果一个字符串是从上述规则导出的,那么它也应该是一个正则表达式。
正则表达式的示例
下表显示了一些正则表达式的示例:
| 正则表达式 | 正则集 |
|---|---|
| (0 + 10*) | {0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | {ε, 0, 1, 01} |
| (a+b)* | 它将是任意长度的 a 和 b 字符串集,也包括空字符串,即 {ε, a, b, aa, ab, bb, ba, aaa……}。 |
| (a+b)*abb | 它将是 a 和 b 字符串集,以字符串 abb 结尾,即 {abb, aabb, babb, aaabb, ababb, …………..}。 |
| (11)* | 它将是包含偶数个 1 的字符串集,也包括空字符串,即 {ε, 11, 1111, 111111, ………}。 |
| (aa)*(bb)*b | 它将是包含偶数个 a 后跟奇数个 b 的字符串集,即 {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..}。 |
| (aa + ab + ba + bb)* | 它将是偶数长度的 a 和 b 字符串,可以通过串联 aa、ab、ba 和 bb 的任何组合(包括空字符串)获得,即 {aa, ab, ba, bb, aaab, aaba, …………..}。 |
正则集及其属性
它可以定义为表示正则表达式值的集合,并具有特定属性。
正则集的属性
如果我们对两个正则集进行并集运算,则结果集也应该是正则的。
如果我们对两个正则集进行交集运算,则结果集也应该是正则的。
如果我们对正则集进行补集运算,则结果集也应该是正则的。
如果我们对两个正则集进行差集运算,则结果集也应该是正则的。
如果我们对正则集进行反转运算,则结果集也应该是正则的。
如果我们对正则集进行闭包运算,则结果集也应该是正则的。
如果我们对两个正则集进行串联运算,则结果集也应该是正则的。
有限状态自动机
术语自动机源于希腊语“αὐτόματα”,意思是“自动的”,是自动机的复数形式,可以定义为一种抽象的自动推进计算设备,它会自动遵循预定的操作序列。
具有有限数量状态的自动机称为有限自动机 (FA) 或有限状态自动机 (FSA)。
数学上,自动机可以用一个 5 元组 (Q, Σ, δ, q0, F) 来表示,其中:
Q 是有限的状态集。
Σ 是有限的符号集,称为自动机的字母表。
δ 是转移函数
q0 是处理任何输入的初始状态 (q0 ∈ Q)。
F 是 Q 的最终状态集 (F ⊆ Q)。
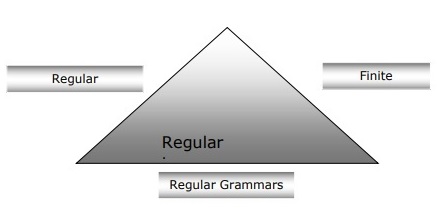
有限自动机、正则文法和正则表达式之间的关系
以下几点将使我们更清楚地了解有限自动机、正则文法和正则表达式之间的关系:
众所周知,有限状态自动机是计算工作的理论基础,正则表达式是描述它们的一种方式。
我们可以说,任何正则表达式都可以实现为 FSA,任何 FSA 都可以用正则表达式来描述。
另一方面,正则表达式是一种表征称为正则语言的语言类型的方式。因此,我们可以说正则语言可以用 FSA 和正则表达式来描述。
正则文法(可以是右正则或左正则的形式文法)是表征正则语言的另一种方式。
下图显示有限自动机、正则表达式和正则文法是描述正则语言的等效方式。
有限状态自动机 (FSA) 的类型
有限状态自动机分为两种类型。让我们看看这些类型是什么。
确定性有限自动机 (DFA)
它可以定义为一种有限自动机,其中对于每个输入符号,我们可以确定机器将移动到的状态。它具有有限数量的状态,这就是为什么机器被称为确定性有限自动机 (DFA) 的原因。
数学上,DFA 可以用一个 5 元组 (Q, Σ, δ, q0, F) 来表示,其中:
Q 是有限的状态集。
Σ 是有限的符号集,称为自动机的字母表。
δ 是转移函数,其中 δ: Q × Σ → Q。
q0 是处理任何输入的初始状态 (q0 ∈ Q)。
F 是 Q 的最终状态集 (F ⊆ Q)。
而在图形上,DFA 可以用称为状态图的有向图来表示,其中:
状态由顶点表示。
转换由带标签的弧表示。
初始状态由空的传入弧表示。
最终状态由双圆圈表示。
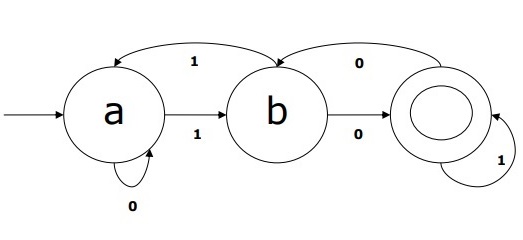
DFA 示例
假设一个 DFA 为
Q = {a, b, c},
Σ = {0, 1},
q0 = {a},
F = {c},
转移函数 δ 如表所示:
| 当前状态 | 输入 0 的下一状态 | 输入 1 的下一状态 |
|---|---|---|
| A | a | B |
| B | b | A |
| C | c | C |
此 DFA 的图形表示如下:
非确定性有限自动机 (NDFA)
它可以定义为一种有限自动机,其中对于每个输入符号,我们无法确定机器将移动到的状态,即机器可以移动到任何状态组合。它具有有限数量的状态,这就是为什么机器被称为非确定性有限自动机 (NDFA) 的原因。
数学上,NDFA 可以用一个 5 元组 (Q, Σ, δ, q0, F) 来表示,其中:
Q 是有限的状态集。
Σ 是有限的符号集,称为自动机的字母表。
δ:- 是转移函数,其中 δ: Q × Σ → 2Q。
q0:- 是处理任何输入的初始状态 (q0 ∈ Q)。
F:- 是 Q 的最终状态集 (F ⊆ Q)。
而在图形上(与 DFA 相同),NDFA 可以用称为状态图的有向图来表示,其中:
状态由顶点表示。
转换由带标签的弧表示。
初始状态由空的传入弧表示。
最终状态由双圆圈表示。
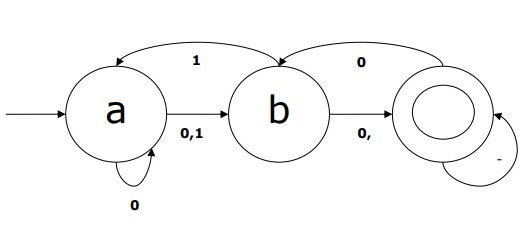
NDFA 示例
假设一个 NDFA 为
Q = {a, b, c},
Σ = {0, 1},
q0 = {a},
F = {c},
转移函数 δ 如表所示:
| 当前状态 | 输入 0 的下一状态 | 输入 1 的下一状态 |
|---|---|---|
| A | a, b | B |
| B | C | a, c |
| C | b, c | C |
此 NDFA 的图形表示如下:
形态分析
术语形态分析与词素的分析有关。我们可以将形态分析定义为识别单词分解成称为词素的较小有意义单元的问题,从而为其产生某种语言结构。例如,我们可以将单词 *foxes* 分解成两个,*fox* 和 *-es*。我们可以看到,单词 *foxes* 由两个词素组成,一个是 *fox*,另一个是 *-es*。
换句话说,我们可以说形态学是研究:
单词的构成。
单词的起源。
单词的语法形式。
在单词构成中使用前缀和后缀。
语言的词性是如何构成的。
词素的类型
词素是最小的意义单元,可以分为两种类型:
词干
词序
词干
它是单词的核心有意义的单元。我们也可以说它是单词的词根。例如,在单词 foxes 中,词干是 fox。
词缀 - 顾名思义,它们为单词添加了一些额外的含义和语法功能。例如,在单词 foxes 中,词缀是 -es。
此外,词缀还可以细分为以下四种类型:
前缀 - 顾名思义,前缀位于词干之前。例如,在单词 unbuckle 中,un 是前缀。
后缀 - 顾名思义,后缀位于词干之后。例如,在单词 cats 中,-s 是后缀。
中缀 - 顾名思义,中缀插入词干内部。例如,单词 cupful 可以通过使用 -s 作为中缀变为复数 cupsful。
环绕词缀 - 它们位于词干之前和之后。英语中环绕词缀的例子很少。一个非常常见的例子是“A-ing”,其中我们可以使用 -A 位于词干之前,-ing 位于词干之后。
词序
词序将由形态分析决定。现在让我们看看构建形态分析器的要求:
词典
构建形态分析器的第一个要求是词典,其中包括词干和词缀的列表以及关于它们的 基本信息。例如,诸如词干是名词词干还是动词词干等信息。
形态句法
它基本上是词素排序模型。换句话说,解释哪些词素类可以在单词内部跟随其他词素类的模型。例如,形态句法事实是,英语复数词素总是跟在名词后面,而不是在名词前面。
拼写规则
这些拼写规则用于模拟单词中发生的更改。例如,将 y 转换为 ie 的规则,例如 city+s = cities,而不是 citys。