数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究二叉树中等腰三角形的数量
二叉树是一种数据结构，其中每个节点最多可以有两个子节点。这两个子节点分别称为左子节点和右子节点。假设我们给定一个父节点数组表示，使用该数组可以创建一个二叉树。二叉树可能包含多个等腰三角形。我们必须找到该二叉树中所有可能的等腰三角形的总数。
在本文中，我们将探讨在 C++ 中解决此问题的几种技术。
理解问题
给定一个父节点数组。您必须将其表示为二叉树的形式，以便数组索引形成树节点的值，而数组中的值给出该特定索引的父节点。
请注意，-1 将始终是根父节点。下面是一个数组及其二叉树表示。
Parent array = [0, -1, 3, 1, 1, 2, 2, 3, 4, 4]
二叉树 -
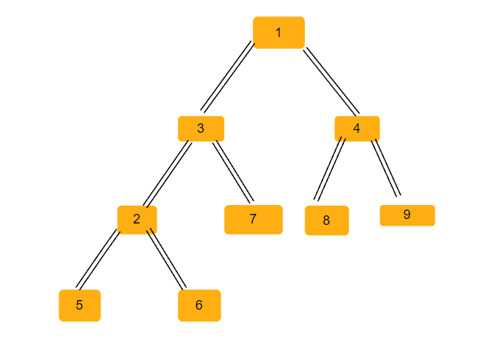
在任何二叉树中，我们都可以找到三种类型的等腰三角形 -
左等腰三角形 − 在这个三角形中，顶点是父节点的左子节点，而构成底边的顶点（等腰三角形的等边）是顶点的左子节点。子节点可以是直接的或间接的。在上图中，我们有两个这样的等腰三角形 - (2, 6, 3), (3, 7, 1)。
右等腰三角形 − 在这个三角形中，顶点是父节点的右子节点，而构成底边的顶点是顶点的右子节点。子节点可以是直接的或间接的。在上图中，我们只有一个这样的等腰三角形 (4, 1, 8)。
平衡等腰三角形 − 在这个三角形中，构成底边的顶点是顶点节点的左子节点和右子节点。在上图中，我们有五个这样的等腰三角形 (1, 3, 4), (3, 2, 7), (4, 8, 9), (2, 5, 6), (1, 2, 9)
因此，对于上面的二叉树，我们总共有8 个等腰三角形。
使用深度优先搜索遍历
深度优先搜索 (DFS) 是一种以深度优先的方式遍历树的所有节点的方法。它从根节点开始，移动到每个分支，然后回溯。
首先，我们使用DFS遍历二叉树的每个节点，该二叉树被转换为图，以便每个节点都彼此相邻。这使得遍历更容易。
对于每个节点，我们检查它是否具有任何子节点。检查后，它使用sort(node[x].begin(), node[x].end())函数对它们进行排序。
接下来，我们检查当前节点是否为其相应父节点的左或右后继。我们对二叉树的所有节点递归使用 DFS 函数。
如果当前节点有两个子节点（直接或间接），我们通过计算它们之间的边来检查是否存在等腰三角形的可能性。我们将通过下面代码中给出的graph函数找到它们之间的边。
最后，我们通过将来自不同位置的所有可能的三角形加起来来计算等腰三角形的总数。
示例
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
#define MAX int(1e5)
vector < int > * node;
int right_down[MAX];
int right_up[MAX];
int left_down[MAX];
int left_up[MAX];
// DFS traversal over a node
void DFS(int x, int * parent) {
// Check if adjacent nodes are present for node x
if (node[x].size() != 0)
sort(node[x].begin(), node[x].end());
// Check whether the node has a parent node
if (parent[x] != -1) {
int indexOfParent = parent[x];
int childrenCount = node[indexOfParent].size();
if (childrenCount > 1) {
int parentFirstChild = node[indexOfParent][0];
// Check if current node is left node of the parent
if (x == parentFirstChild) {
right_up[x] += right_up[indexOfParent] + 1;
// Check if current node is right node of the parent
} else {
left_up[x] += left_up[indexOfParent] + 1;
}
} else {
right_up[x] += right_up[indexOfParent] + 1;
}
}
// Iterate over children of current node
for (int i = 0; i < node[x].size(); ++i) {
int y = node[x][i];
DFS(y, parent);
// left child of current node
if (i == 0) {
left_down[x] += left_down[y] + 1;
}
// right child of current node
else {
right_down[x] += right_down[y] + 1;
}
}
}
int graph(int * parent, int N) {
int rootNode;
node = new vector < int > [N];
for (int i = 0; i < N; ++i) {
if (parent[i] != -1) {
node[parent[i]].push_back(i);
} else {
rootNode = i;
}
left_up[i] = 0;
right_up[i] = 0;
left_down[i] = 0;
right_down[i] = 0;
}
return rootNode;
}
int main() {
int N = 10;
int parent[] = { 0, -1, 3, 1, 1, 2, 2, 3, 4, 4 };
int rootNode = graph(parent, N);
DFS(rootNode, parent);
int count = 0;
// Counting the total isosceles triangles
for (int i = 0; i < N; ++i) {
count += min(right_down[i], right_up[i]);
count += min(left_down[i], left_up[i]);
count += min(left_down[i], right_down[i]);
}
cout << "Number of isosceles triangles in the binary tree are " <<
count;
return 0;
}
输出
Number of isosceles triangles in the binary tree are 8
结论
我们讨论了如何在给定父节点数组的情况下找到二叉树中等腰三角形的总数。我们可以通过使用深度优先搜索来做到这一点，深度优先搜索允许我们遍历二叉树。
105 次查看
