纵坐标

---

简介

纵坐标是有序对 (x, y) 中的第二个分量。数学有两个主要分支，包括代数和几何。两者都有各自的用途和应用。然而，法国数学家勒内·笛卡尔通过代数和几何的结合推导出了一个概念。这个概念帮助我们表达坐标系中任何物体、点或线的的位置。然而，坐标系中包含各种主题。在本教程中，我们将学习坐标系、笛卡尔平面、其组成部分（纵坐标和横坐标）以及一些带有已解决示例的基本公式。

坐标系

在欧几里得空间中，可以在坐标系上指定任何点的方位。数学中常用的坐标系有四种类型。

• 数轴 − 数轴是一条直线，零右侧包含正整数，零左侧包含负整数。

• 笛卡尔平面 − 笛卡尔平面包含两条带有整数刻度的垂直线段。

• 极坐标系 − 在这种类型的坐标系中，点表示为 (𝑟, 𝜃) 的形式。

• 圆柱坐标系和球坐标系 − 在这种类型的坐标系中，点的极坐标表示为 (𝑟, 𝜃, 𝜙) 的形式。

笛卡尔平面

笛卡尔平面包含两条带有整数刻度的垂直线段。任何点都可以用成对的坐标表示，例如 (x, y)。x 表示 X 轴坐标，y 表示 Y 轴坐标。笛卡尔平面的示意图如下所示。

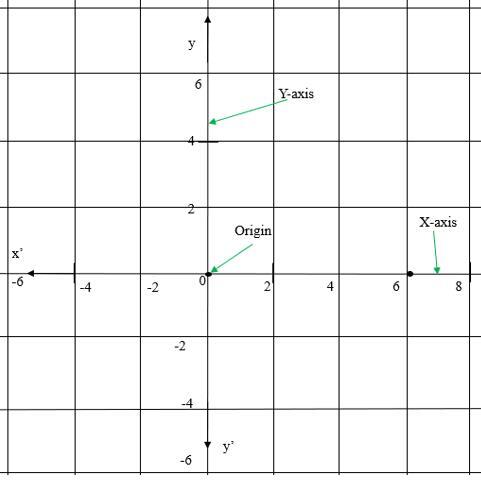
坐标平面中有三个组成部分。

• 轴 − 水平和垂直轴分别称为 X 轴和 Y 轴。

• 原点 − 平面两条轴相交的点称为原点。原点的坐标为 (0, 0)。

• 象限 − 笛卡尔平面上有四个象限，如下图所示

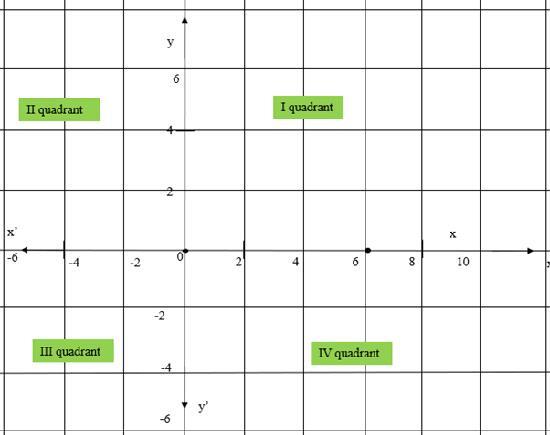
纵坐标

我们知道，任何点都可以用成对的坐标表示，例如 (x, y)。坐标的第二项或分量称为纵坐标。换句话说，点的 Y 轴坐标被称为该点的纵坐标。例如，一个点的坐标是 (6, -4)。该点的纵坐标为 -4。象限决定了点纵坐标的符号。

• 第一象限，y > 0

• 第二象限，y > 0

• 第三象限，y < 0

• 第四象限，y < 0

横坐标

坐标的第一项或分量称为横坐标。换句话说，点的 X 轴坐标被称为该点的横坐标。例如，一个点的坐标是 (4, -5)。该点的横坐标为 4。象限决定了点横坐标的符号。

• 第一象限，x > 0

• 第二象限，x < 0

• 第三象限，x < 0

• 第四象限，x > 0

距离公式

线段的长度也可以使用距离公式计算。在笛卡尔几何中，一个点表示为 (x, y)（其中 x = X 轴值，y = Y 轴值）。线段两个端点的坐标可以表示为 A(𝑥1, 𝑦1) 和 B(𝑥2, 𝑦2)。然后，根据距离公式，可以使用以下表达式获得线段的长度。

$$\mathrm{\overline{AB}\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$

分割公式

我们知道，通常使用点将线段分成两部分。因此，在坐标几何中确定分割点的位置称为分割公式。坐标几何中存在两种类型的分割公式，例如：

• 内分割公式

• 外分割公式

现在，我们将详细讨论每个分割公式。

内分割公式

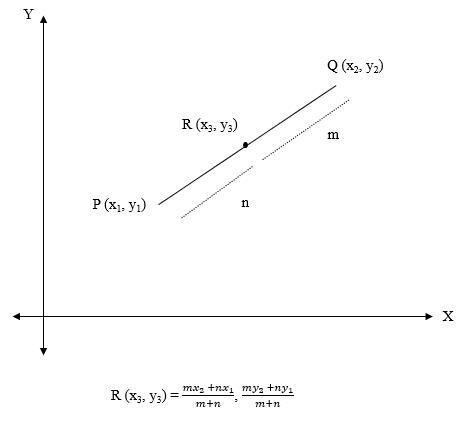
例如，考虑一条线段，其端点的坐标为 𝑃(𝑥1, 𝑦1) 和 𝑄(𝑥2, 𝑦2)。点 𝑅(𝑥3, 𝑦3) 在线段上被内分割，比例为 m:n（如图所示）。现在，可以使用以下公式确定点 𝑅(𝑥3, 𝑦3) 的坐标。

$$\mathrm{R(x_{3}\:,\:y_{3})\:=\:(\frac{mx_{2}\:+\:nx_{1}}{m\:+\:n}\:,\:\frac{my_{2}\:+\:ny_{1}}{m\:+\:n})}$$

外分割公式

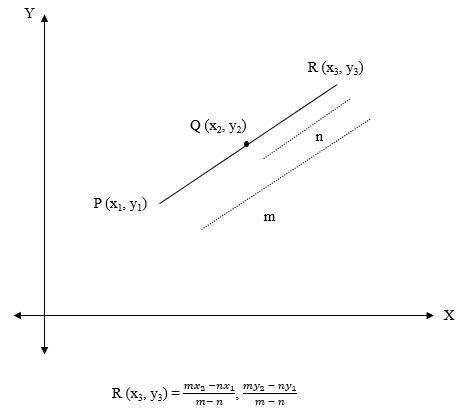
例如，考虑一条线段，其端点的坐标为 𝑃(𝑥1, 𝑦1) 和 𝑄(𝑥2, 𝑦2)。点 𝑅(𝑥3, 𝑦3) 在线段上被外分割，比例为 m:n（如图所示）。现在，可以使用以下公式确定点 𝑅(𝑥3, 𝑦3) 的坐标。

$$\mathrm{R(x_{3}\:,\:y_{3})\:=\;(\frac{mx_{2}\:-\:nx_{1}}{m\:-\:n}\:,\:\frac{my_{2}\:-\:ny_{1}}{m\:-\:n})}$$

面积公式

下面列出了确定各种几何结构面积的公式。

序号	几何图形	面积公式	变量
1	正方形	$\mathrm{a\times\:a\:=\:a^{2}}$	a = 正方形的边长
2	矩形	$\mathrm{l\times\:b}$	l = 长度 b = 宽度
3	圆形	$\mathrm{\pi\:\times\:r^{2}}$	r = 圆的半径
4	三角形	$\mathrm{\frac{1}{2}\times\:b\times\:h}$	b = 三角形的底 h = 三角形的高
5	梯形	$\mathrm{\frac{1}{2}\times\:(a\:+\:b)\times\:h}$	a = 底边长度 (1) b = 底边长度 (2) h = 高度
6	椭圆	$\mathrm{\pi\:\times\:a\:\times\:b}$	a = 长轴半径 b = 短轴半径

已解决示例

1)线段端点的笛卡尔坐标为 A (0, -4) 和 B(3, 6)。计算 𝑨𝑩 的长度。

答案 - 给定端点的坐标为 A (0, -4) 和 B(3, 6)。

根据距离公式，线段的长度将为

$$\mathrm{\overline{AB}\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}}}$$

这里，$\mathrm{x_{1}\:=\:0\:,\:x_{2}\:=\:3\:,\:y_{1}\:=\:-4\:,\:y_{2}\:=\:6}$

现在，$\mathrm{\overline{AB}\:=\:\sqrt{(3\:-\:0)^{2}\:+\:(6\:-\:(-4))^{2}}}$

$\mathrm{\overline{AB}\:=\:\sqrt{(3)^{2}\:+\:(10)^{2}}}$

$\mathrm{\overline{AB}\:=\:\sqrt{109}\:\simeq\:10.44\:cm}$

∴ 线段的长度为 10.44 厘米

2)线段端点的坐标为 (-10, 5) 和 (7, -3)。x 轴上的一点以 m:n 的比例外分割线段。求 m:n 的值

答案 - 给定，

线段端点的坐标 = (-10, 5) 和 (7, 3)

与标准坐标比较，$\mathrm{x_{1}\:=-10\:,\:x_{2}\:=\:7\:,\:y_{2}\:=\:3}$

外部分割比例 = m:n

由于该点位于 x 轴上，因此该点的 y 坐标为 0。

使用外分割公式，

$$\mathrm{R(x_{3}\:,\:y_{3})\:=\:(\frac{mx_{2}\:-\:nx_{1}}{m\:-\:n}\:,\:\frac{my_{2}\:-\:ny_{1}}{m\:-\:n})}$$

$$\mathrm{R(x_{3}\:,\:0)\:=\:(\frac{m\times\:7\:-\:n\times\:(-10)}{m\:-\:n}\:,\:\frac{m\times\:(3)\:-\:n\times\:5}{m\:-\:n})}$$

$$\mathrm{R(x_{3}\:,\:0)\:=\:\frac{7m\:+\:10n}{m\:-\:n}\:,\:\frac{3m\:-\:5n}{m\:-\:n}}$$

现在，比较两边的 y 坐标，我们得到

$$\mathrm{\frac{3m\:-\:5n}{m\:-\:n}\:=\:0}$$

$$\mathrm{\Longrightarrow\:3m\:-\:5n\:=\:0\times\:(m\times\:n)\:=\:0}$$

$$\mathrm{\Longrightarrow\:3m\:=\:5n}$$

$$\mathrm{\Longrightarrow\:\frac{m}{n}\:=\:\frac{5}{3}}$$

∴给定点以 5:3 的比例外分割线段。

结论

本教程简要介绍了坐标系及其各种组成部分。本教程阐述了坐标系、笛卡尔平面、纵坐标和横坐标的基本定义。此外，还说明了确定两点之间距离、分割公式和面积公式的过程。此外，还提供了一些已解决示例，以便更好地理解此概念。总之，本教程可能有助于理解纵坐标和坐标系的基本概念。

常见问题

1. 确定给定点的象限：(7, -9)。

由于x坐标为正，y坐标为负，因此该点位于第四象限。

2. 原点的坐标是什么？

在笛卡尔平面中，原点的坐标为 (0, 0)。

3. 在坐标系中绘制点时，应先往哪个方向移动？

在笛卡尔平面上定位点时，我们应该先定位x坐标。然后，我们定位y坐标。

4. 我们能使用截距公式确定线段的长度吗？

不能，我们必须应用距离公式来确定线段的长度。

5. 在截距公式中，比例m:n可以为负值吗？

可以。在外分时，比例m:n为负值。