自耦变压器的输出和变压器铜材的节省

自耦变压器的运行原理

理想降压自耦变压器的连接图如图所示。其中绕组ab是初级绕组，有N₁匝；绕组bc是次级绕组，有N₂匝。这里，I₁是输入初级电流，I₂是输出次级电流或负载电流。

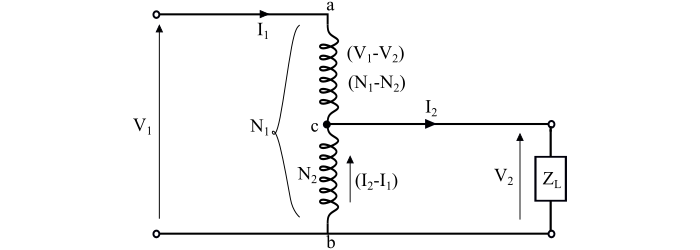
现在，绕组'ac'部分的匝数为N₁ – N₂匝，该部分的电压为V₁ – V₂。公共部分（绕组'bc'）中的电流为I₂ – I₁。

考虑如图所示的自耦变压器的等效电路。从这个等效电路中，我们得到：

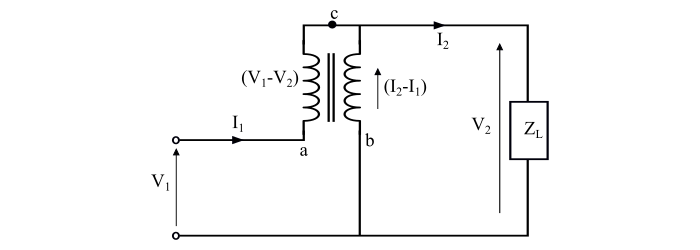
$$\mathrm{\frac{𝑉_{2}}{𝑉_{1}\:−\:𝑉_{2}}=\frac{𝑁_{2}}{𝑁_{1}\:−\:𝑁_{2}}}$$

$$\mathrm{\Rightarrow\:𝑁_{1}𝑉_{2}\:−\:𝑁_{2}𝑉_{2} = 𝑁_{2}𝑉_{1}\:−\:𝑁_{2}𝑉_{2}}$$

$$\mathrm{\Rightarrow\:𝑁_{1}𝑉_{2} = 𝑁_{2}𝑉_{1}}$$

$$\mathrm{\Rightarrow\:\frac{𝑉_{2}}{𝑉_{1}}=\frac{𝑁_{2}}{𝑁_{1}}= 𝑎_{𝐴}… (1)}$$

公式(1)称为自耦变压器的电压变换比。

此外，从自耦变压器的等效电路中，我们有：

$$\mathrm{(𝑉_{1}\:−\:𝑉_{2})𝐼_{1}= 𝑉_{2}(𝐼_{2}\:−\:𝐼_{1})}$$

$$\mathrm{\Rightarrow\:𝑉_{1}𝐼_{1}\:−\:𝑉_{2}𝐼_{1} = 𝑉_{2}𝐼_{2}\:−\:𝑉_{2}𝐼_{1}}$$

$$\mathrm{\Rightarrow\:𝑉_{1}𝐼_{1}\:=\:𝑉_{2}𝐼_{2}}$$

$$\mathrm{\Rightarrow\:\frac{𝑉_{2}}{𝑉_{1}}=\frac{𝐼_{1}}{𝐼_{2}}… (2)}$$

从公式(1)和(2)，我们得到：

$$\mathrm{\frac{𝑉_{2}}{𝑉_{1}}=\frac{𝑁_{2}}{𝑁_{1}}=\frac{𝐼_{1}}{𝐼_{2}}= 𝑎_{𝐴}… (3)}$$

由于给定的自耦变压器是理想的，因此：

$$\mathrm{𝑉_{1}𝐼_{1}\:=\:𝑉_{2}𝐼_{2}… (4)}$$

$$\mathrm{\Rightarrow\: 输入视在功率 = 输出视在功率}$$

自耦变压器的输出

由于自耦变压器的初级和次级绕组既有磁连接也有电连接。因此，功率从初级侧传递到次级侧既有磁性（感应）方式，也有传导方式。

这里：

$$\mathrm{输出视在功率 = 𝑉_{2}𝐼_{2}}$$

$$\mathrm{感应传递功率\:= \:𝑉_{2}(𝐼_{2}\:−\:𝐼_{1})}$$

$$\mathrm{∵\:𝐼_{1}\:=\:𝑎_{𝐴}𝐼_{2}}$$

$$\mathrm{∴\:感应传递功率 = 𝑉_{2}(𝐼_{2}\:−\:𝑎_{𝐴}𝐼_{2}) = 𝑉_{2}𝐼_{2}(1\:−\:𝑎_{𝐴})}$$

由于：

$$\mathrm{𝑉_{1}𝐼_{1}\:=\:𝑉_{2}𝐼_{2}}$$

因此：

$$\mathrm{感应传递功率 \:=\:𝑉_{1}𝐼_{1}(1\:−\:𝑎_{𝐴}) = 输入功率 × (1\:− \:𝑎_{𝐴}) … (5)}$$

公式(5)给出了从初级到次级磁性传递的功率量。

现在，传导传递的功率由下式给出：

$$\mathrm{传导传递功率\:=\\: (输入功率)\:−\:(感应传递功率)}$$

$$\mathrm{\Rightarrow\:传导传递功率 = (输入功率)\:−\:[输入功率\:×\:(1\:−\:𝑎_{𝐴})]}$$

$$\mathrm{= 输入功率\:×\:(1\:−\:(1\:−\:𝑎_{𝐴}))}$$

$$\mathrm{传导传递功率 = 输入功率\:×\:𝑎_{𝐴}… (6)}$$

公式(6)给出了从初级到次级电传导的功率量。

变压器导体材料（铜）的节省

对于相同的额定值，即相同的输出和相同的变比，与普通的双绕组变压器相比，自耦变压器需要的导体材料（铜）更少。该图显示了一个双绕组变压器（左）和一个自耦变压器（右），两者额定值相同。

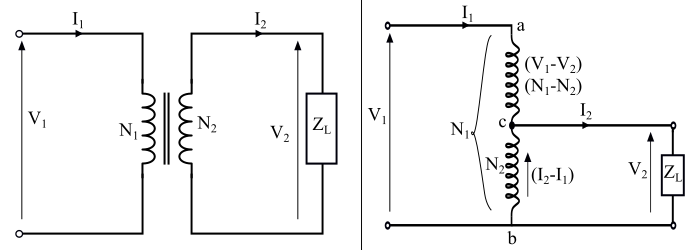
绕组中所需的铜线长度与绕组的匝数成正比，导线的横截面积与电流额定值成正比。因此，绕组中所需的铜材料的体积和重量与电流和绕组匝数的乘积成正比，即：

$$\mathrm{所需铜材重量 \:∝\:电流 × 匝数}$$

对于双绕组变压器：

$$\mathrm{所需铜材重量\:∝ \:(𝐼_{1}𝑁_{1}+ 𝐼_{2}𝑁_{2})}$$

对于自耦变压器：

$$\mathrm{ac段所需铜材重量\:∝\:𝐼_{1}(𝑁_{1} − 𝑁_{2})}$$

$$\mathrm{bc段所需铜材重量\:∝\:(𝐼_{2} − 𝐼_{1})𝑁_{2}}$$

因此：

$$\mathrm{所需铜材总重量 \:∝ [𝐼_{1}(𝑁_{1} − 𝑁_{2}) + (𝐼_{2} − 𝐼_{1})𝑁_{2}]}$$

现在，比较自耦变压器和双绕组变压器所需的铜材重量，我们得到：

$$\mathrm{\frac{自耦变压器所需铜材重量\:(𝑊_{𝑎})}{双绕组变压器所需铜材重量\:(𝑊𝑜)}\=\frac{[𝐼_{1}(𝑁_{1} − 𝑁_{2}) + (𝐼_{2} − 𝐼_{1})𝑁_{2}]}{(𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2})}}$$

$$\mathrm{\Rightarrow\:\frac{𝑊_{𝑎}}{𝑊_{𝑜}}=\frac{𝐼_{1}𝑁_{1} − 𝐼_{1}𝑁_{2} + 𝐼_{2}𝑁_{2} − 𝐼_{1}𝑁_{2}}{𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2}}=\frac{𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2} − 2𝐼_{1}𝑁_{2}}{𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2}}}$$

$$\mathrm{\Rightarrow\:\frac{𝑊_{𝑎}}{𝑊_{𝑜}}=1-\frac{2𝐼_{1}𝑁_{2}}{𝐼_{1}𝑁_{1} + 𝐼_{2}𝑁_{2}}}$$

$$\mathrm{∵\:𝐼_{2}𝑁_{2}= 𝐼_{1}𝑁_{1}}$$

$$\mathrm{\Rightarrow\:\frac{𝑊_{𝑎}}{𝑊_{𝑜}}=1-\frac{2𝐼_{1}𝑁_{2}}{2𝐼_{1}𝑁_{1}}=1-\frac{𝑁_{2}}{𝑁_{1}}= (1 − 𝑎_{𝐴})}$$

因此，自耦变压器所需的铜材重量为

$$\mathrm{(自耦变压器所需铜材重量\:(𝑊_{𝑎})) =\ (1 − 𝑎_{𝐴}) ×(双绕组变压器所需铜材重量\:(𝑊_{𝑜})) … (7)}$$

因此，与双绕组变压器相比，自耦变压器中铜材的节省量由下式给出：

$$\mathrm{铜材节省量 = 𝑊_{𝑜 }− 𝑊_{𝑎} = 𝑊_{𝑜} − (1 − 𝑎_{𝐴})𝑊_{𝑜}}$$

$$\mathrm{\Rightarrow\:铜材节省量 = 𝑎_{𝐴} × 𝑊_{𝑜} … (8)}$$

公式(8)给出了自耦变压器中铜材节省量的值。很明显，自耦变压器的𝑎_𝐴值越接近1，铜材的节省量就越大。

Saini Manish Kumar

更新于：2021年8月12日

浏览量：3000+

启动您的职业生涯

完成课程获得认证

开始学习