给出对顶角定理的证明。

定理

在两条相交直线中，对顶角相等。

证明

让我们考虑两条在 $O$ 点相交的直线 $AB$ 和 $CD$。

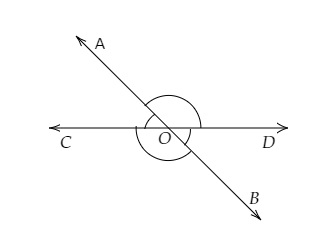
$\angle AOD$ 和 $\angle AOC$ 构成一个线性对。

因此，

$\angle AOD + \angle AOC = 180^o$........(i)

$\angle AOC$ 和 $\angle BOC$ 构成一个线性对。

因此，

$\angle AOC + \angle BOC = 180^o$........(ii)

由 (i) 和 (ii)，

$\angle AOD + \angle AOC = \angle AOC + \angle BOC$

$\Rightarrow \angle AOD = \angle BOC$.........(iii)

$\angle AOD$ 和 $\angle BOD$ 构成一个线性对。

因此，

$\angle AOD + \angle BOD = 180^o$........(iv)

由 (i) 和 (iv)，

$\angle AOD + \angle AOC = \angle AOD + \angle BOD$

$\Rightarrow \angle AOC = \angle BOD$

因此，一对对顶角相等。

证毕。

教程点

更新于: 2022年10月10日

94 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习