并行算法 - 矩阵乘法

矩阵是由按固定行数和列数排列的数值和非数值数据组成的集合。矩阵乘法是并行计算中一种重要的乘法设计。在这里，我们将讨论在各种通信网络（如网格和超立方体）上实现矩阵乘法的方案。网格和超立方体具有更高的网络连接性，因此它们允许比其他网络（如环形网络）更快的算法。

网格网络

一组节点形成一个 p 维网格的拓扑结构称为网格拓扑结构。在这里，所有边都平行于网格轴，并且所有相邻节点都可以相互通信。

节点总数 =（行中的节点数）×（列中的节点数）

可以使用以下因素评估网格网络：

直径
二分宽度

直径 - 在网格网络中，两个节点之间最长的距离即为其直径。具有kP个节点的 p 维网格网络的直径为p(k–1)。

二分宽度 - 二分宽度是从网络中移除以将网格网络分成两半所需的最小边数。

使用网格网络进行矩阵乘法

我们考虑了一个具有环绕连接的二维网格网络 SIMD 模型。我们将设计一种算法，使用 n² 个处理器在特定时间内乘以两个 n × n 数组。

矩阵 A 和 B 的元素分别为 a_ij 和 b_ij。处理单元 PE_ij 表示 a_ij 和 b_ij。以这样的方式排列矩阵 A 和 B，使得每个处理器都有一对要相乘的元素。矩阵 A 的元素将向左移动，矩阵 B 的元素将向上移动。矩阵 A 和 B 中元素位置的这些变化为每个处理单元 PE 提供了一对新的要相乘的值。

算法步骤

交错两个矩阵。
计算所有乘积，a_ik × b_kj
在步骤 2 完成后计算总和。

算法

Procedure MatrixMulti

Begin
   for k = 1 to n-1
	
   for all Pij; where i and j ranges from 1 to n
      ifi is greater than k then
         rotate a in left direction
      end if
		
   if j is greater than k then
      rotate b in the upward direction
   end if
	
   for all Pij ; where i and j lies between 1 and n
      compute the product of a and b and store it in c
   for k= 1 to n-1 step 1
   for all Pi;j where i and j ranges from 1 to n
      rotate a in left direction
      rotate b in the upward direction
      c=c+aXb
End

超立方体网络

超立方体是一个 n 维结构，其中边彼此垂直且长度相同。n 维超立方体也称为 n-cube 或 n 维立方体。

具有 2^k 个节点的超立方体的特征

直径 = k
二分宽度 = 2^k–1
边数 = k

使用超立方体网络进行矩阵乘法

超立方体网络的一般规范：

令N = 2^m为处理器总数。令处理器为 P_0, P₁…..P_N-1。
令 i 和 i^b 为两个整数，0 < i,i^b < N-1，并且它们的二进制表示仅在位置 b 不同，0 < b < k–1。
让我们考虑两个 n × n 矩阵，矩阵 A 和矩阵 B。
步骤 1 - 矩阵 A 和矩阵 B 的元素被分配给 n³ 个处理器，使得位置 i、j、k 处的处理器具有 a_ji 和 b_ik。
步骤 2 - 位置 (i,j,k) 处的所有处理器都计算乘积

C(i,j,k) = A(i,j,k) × B(i,j,k)
步骤 3 - C(0,j,k) = ΣC(i,j,k)，其中 0 ≤ i ≤ n-1，其中 0 ≤ j, k < n–1。

分块矩阵

分块矩阵或分区矩阵是一个矩阵，其中每个元素本身代表一个单独的矩阵。这些单独的部分称为块或子矩阵。

示例

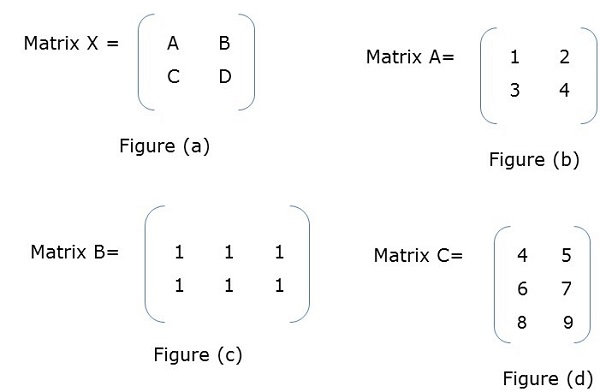
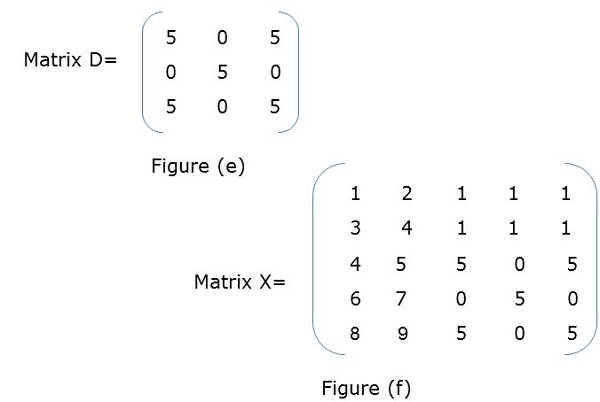
在图 (a) 中，X 是一个分块矩阵，其中 A、B、C、D 本身就是矩阵。图 (f) 显示了整个矩阵。

分块矩阵乘法

当两个分块矩阵是方阵时，它们的乘法方式与我们执行简单矩阵乘法的方式相同。例如，

打印页面