物理 - 球面透镜

介绍

• 由两个表面（其中一个或两个表面是球形的）包围的透明材料（通常是玻璃）称为“球面透镜”。

凸透镜

• 一个透镜可能有两个向外凸起的球面（如下图所示），称为凸透镜或双凸透镜。

• 此透镜的中间部分凸起（较厚），两端较窄。

• 凸透镜会汇聚光线；因此，它也称为**会聚透镜**。

凹透镜

• 一个透镜可能有两个向内弯曲的球面（如下图所示），称为凹透镜或双凹透镜。

• 此透镜的中间部分较窄（向内弯曲），两端较厚。

• 凹透镜会发散光线；因此，它也称为**发散透镜**。

• 一个透镜，无论是凹透镜还是凸透镜，都有两个球面，每个球面都构成球的一部分。这些球的中心称为**曲率中心**，用英文字母“**C**”表示。

• 由于有两个曲率中心，因此分别表示为“C₁”和“C₂”。

• 穿过透镜两个曲率中心的假想直线称为**主轴**。

• 光心是透镜的中心点。它用“**O**”表示。

• 光圈是球面透镜圆形轮廓的实际直径。

• 透镜的主焦点用“**F**”表示。

• 一个透镜通常有两个焦点，分别表示为F₁和F₂。

• **焦距**是透镜的主焦点和光心之间的距离。它用“**f**”表示。

• 下表说明了凸透镜成像的性质和位置：

物体的位 置	像的位置	像的大小	像的性质	成像
无限远	在焦点F2处	高度缩小，点状	实像，倒立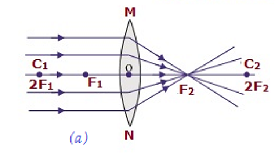
超过2F1	在F2和2F2之间	缩小	实像，倒立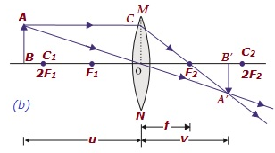
在2F1处	在2F2处	相同大小	实像，倒立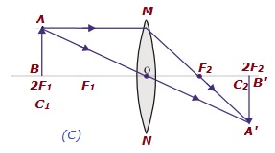
在F1和2F1之间	超过2F2	放大	实像，倒立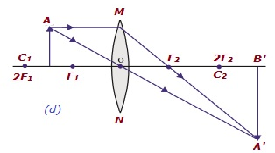
在焦点F1处	无限远	无限大或高度放大	实像，倒立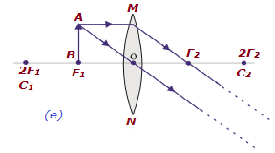
在焦点F1和光心O之间	与物体位于透镜的同一侧	放大	虚像，正立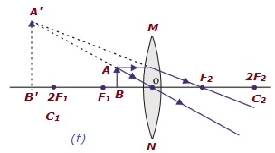

• 下表说明了凹透镜成像的性质和位置：

物体的位 置	像的位置	像的相对大小	像的性质	成像
无限远	在焦点F1处	高度缩小，点状	虚像，正立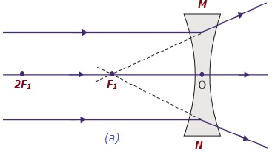
在无限远和透镜的光心O之间	在F1和光心O之间	缩小	虚像，正立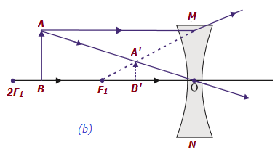

透镜公式

• 公式表示为：

$$ \frac{1}{v} - \frac{1}{u} = \frac{1}{f} $$

• 透镜公式表示物体距离（即**u**）、像距（即**v**）和透镜焦距（即f）之间的关系。