泊松比

---

引言

泊松比是一个非常重要的材料属性，它能告诉我们各种材料在充满的情况下如何变形。让我们以橡皮筋为例。如果你拉伸一根橡皮筋，它的长度会增加，但同时你会看到中间部分会变细。因此，泊松比可以告诉我们橡皮筋会变细多少。

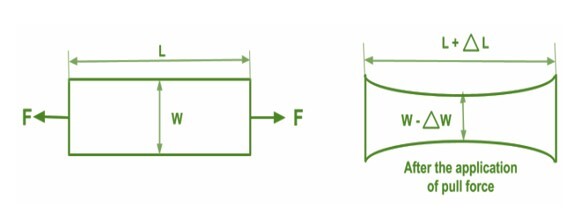
从上图可以看出，L是橡皮筋的原始长度，但在拉伸或施加力后，长度变为L+ΔL，宽度W变为W+ΔW。因此，橡皮筋的厚度变薄了。

什么是泊松比？

泊松比以著名的法国数学家西莫恩·丹尼斯·泊松的名字命名，他于1827年正式解释了这个重要比率。

现在取一个长方体，如果我们对其施加压缩力，它会在垂直于施力方向的方向上膨胀。我们可以定义泊松比，如下面的图表所示：

$$\mathrm{ \varepsilon =\frac{横向应变}{纵向应变}}$$

Cdang, Traction compression deformation sans poisson, CC BY-SA 3.0

我们可以将施力方向称为纵向或x轴方向（位于x轴上），并将垂直方向称为横向方向（位于y轴上）。现在，如果我们反转力的方向以施加拉伸载荷，长方体将在纵向（y轴上）伸长，并在横向（y轴上）收缩。这里的主要概念是，当你在一个方向上对材料施加载荷时，材料会在横向变形。

几何变化的泊松比

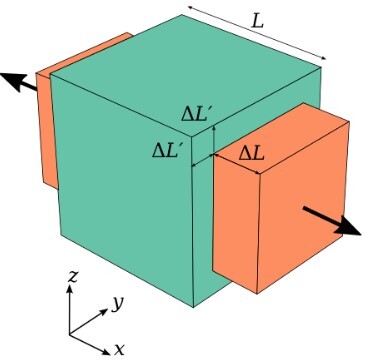
为了更精确地定义泊松比，让我们仔细看看给定的图形，其中施加了拉伸力。首先，我们为这里涉及的各种参数命名。设长度Lx、Ly和Lz为我们沿x、y和z轴取的长方体形状的初始尺寸。现在，$\mathrm{\Delta L_x,\:\Delta L_y \:and\:\Delta L_z }$是施加载荷后这些尺寸发生的改变。此外，尺寸变化发生在物体的两侧。

现在所有三个方向的应变可以写成：

$$\mathrm{\varepsilon_x=-\frac{\Delta L_x}{L_x}\varepsilon_y=-\frac{\Delta L_y}{L_y}\varepsilon_z =-\frac{\Delta L_z}{L_z}}$$

$$\mathrm{其中\:\:\varepsilon=\frac{长度变化}{原始长度}}$$

众所周知：

$$\mathrm{泊松比,ν=\frac {横向应变或横向应变 }{纵向应变或轴向应变}}$$

$$\mathrm{泊松比,ν=\frac{-ε_{横向}}{ε_{纵向}}}$$

这里的负号是因为按照惯例，拉伸应变为正，压缩应变为负。因为那里的符号是负的，这意味着由于横向应变，它的符号与纵向应变相反，这样我们就能得到增加的泊松比。

PAR, PoissonRatio, 标记为公共领域，更多详情请访问维基共享资源

应用

• 当管道内的液体承受极高的压力时，它会在管道内部施加力。这导致管道材料产生应力。由于泊松效应，这种应力导致管道长度增加，而长度略微减小。这会特别影响管道的接头。结果，它会在串联连接的管道每一部分处组装。

• 由于施加的力或应力，地壳中的岩石在垂直方向上膨胀或收缩，从而在x轴上变形，从而导致泊松比。

• 软木的泊松比为0。因此，它具有优势。当软木塞放在瓶子里时，瓶子的上部不会在长度上膨胀，因为它承受压缩。如果瓶塞是由橡胶材料制成的，那么克服上部膨胀所需的额外力会很大，因为那里有橡胶瓶塞。

结论

我们提到的方程式和概念仅适用于各向同性材料，即在所有方向上具有相同属性的材料。对于稳定、各向同性和线性的弹性材料，泊松比必须在-1.0和+0.5之间。但除此之外，泊松比的值是正常的，它介于0.0和0.5之间。

下表显示了一些常见物质的泊松比：

材料	泊松比
铜	0.33
混凝土	0.2
橡胶	0.49

材料	泊松比
软木	0
玻璃	0.18 - 0.3
黄金	0.43
石灰石	0.2 - 0.3

常见问题

1. 金属钢的泊松比是多少？

通常情况下，金属钢的泊松比在0.27到0.30之间。

2. 一根金属丝的纵向应变为0.25，泊松比为0.5。计算该金属丝产生的横向应变。

$$\mathrm{已知：金属丝纵向方向的应变,\: \varepsilon_{纵向} = 0.25}$$

给定金属丝的泊松比 = 0.5

正如我们对泊松比所知：

$$\mathrm{ ν= \frac{横向应变 }{纵向应变}\:or\:ν=\frac{\varepsilon_{横向}}{\varepsilon_{纵向}} }$$

$$\mathrm{0.5=\frac{-横向应变}{0.25} }$$

$$\mathrm{横向应变\: = 0.125}$$

因此，金属丝的横向应变为0.125。

3. 对于金属，泊松比的最大值和最小值是多少？

金属的泊松比标准介于0到0.5之间。该值为正，原因是如果我们在纵向施加力（即纵向应变），则对于这些材料，横向方向的应变将减小。

4. 泊松比的值可能大于1吗？

是的。在某个方向上，各向异性材料的泊松比会大于1。

5. 一根长度为50毫米，宽度为25毫米的钢条。施加25N的力后，钢条长度显著增加到52毫米。计算宽度的变化。

已知：钢条长度，L - 50毫米

钢条宽度，W - 25毫米。

$$\mathrm{宽度的变化写成\:\Delta W.}$$

众所周知，钢的泊松比等于0.3。

纵向应变：

$$\mathrm{\varepsilon_{纵向}=\frac {\Delta L_x}{L_x}=\frac{52-50}{50}=0.04 }$$

众所周知：

$$\mathrm{ ν=\frac{横向应变 }{纵向应变 }}$$

$$\mathrm{0.3=\frac{\frac{dW}{25}}{0.04}}$$

$$\mathrm{dW=0.012×0.04×25}$$

$$\mathrm{dW=0.3 mm}$$

因此，钢条的宽度将减少0.3毫米。

6. 一根长度为5米的金属丝被拉伸了0.5厘米。计算金属丝中产生的横向应变。（金属丝的泊松比，ν = 0.26）

已知：长度，L = 5米

$$\mathrm{长度变化,\Delta L=0.5 cm=5×10^{-3} m}$$

纵向应变：

$$\mathrm{泊松比=\frac{横向应变 }{纵向应变}}$$

$$\mathrm{横向应变=纵向应变×泊松比}$$

$$\mathrm{横向应变=10^{-3}×0.26}$$

$$\mathrm{横向应变=2.6×10^{-4}}$$