
脉冲调制
到目前为止,我们已经讨论了连续波调制。现在是离散信号的时候了。脉冲调制技术处理离散信号。让我们看看如何将连续信号转换为离散信号。称为采样的过程可以帮助我们做到这一点。
采样
将连续时间信号转换为等效离散时间信号的过程称为采样。在采样过程中,持续采样数据的某个瞬间。
下图显示了连续时间信号x(t)和采样信号xs(t)。当x(t)乘以周期性脉冲序列时,得到采样信号xs(t)。
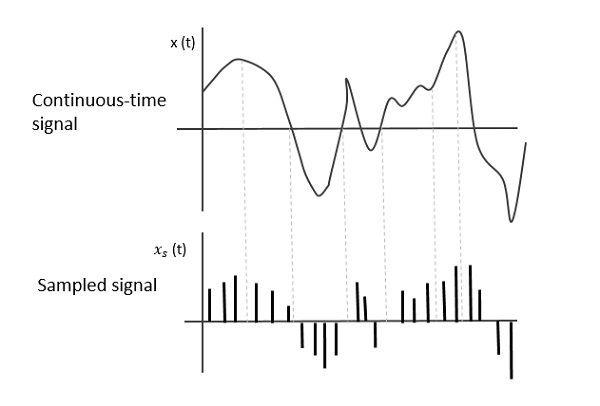
采样信号是脉冲的周期性序列,具有单位幅度,以相等的时间间隔Ts进行采样,称为采样时间。这些数据在时间点Ts传输,载波信号在剩余时间传输。
采样率
为了离散化信号,样本之间的间隙应固定。该间隙可以称为采样周期Ts。
$$采样频率 = \frac{1}{T_s} = f_s$$
其中,
Ts = 采样时间
fs = 采样频率或采样率
采样定理
在考虑采样率时,应该考虑一个关于该速率需要达到多少的重要问题。采样率应使得消息信号中的数据既不会丢失也不会重叠。
采样定理指出,“如果以fs速率对信号进行采样,该速率大于或等于最大频率W的两倍,则可以精确地重现该信号。”
简单来说,为了有效地重现原始信号,采样率应为最高频率的两倍。
这意味着,
$$f_s \geq 2W$$
其中,
fs = 采样频率
W 是最高频率
此采样率称为奈奎斯特率。
采样定理,也称为奈奎斯特定理,根据带宽为带限函数类提供了足够的采样率理论。
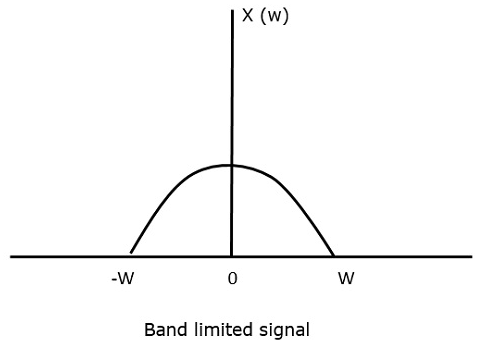
对于连续时间信号x(t),频域中的带限信号可以表示如下面的图所示。
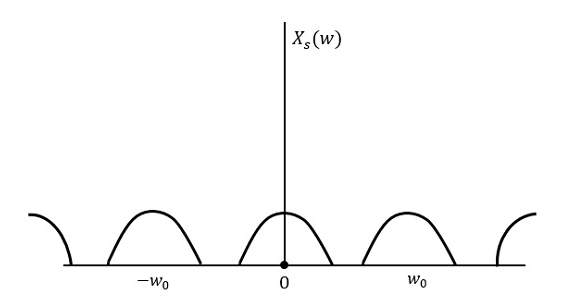
如果信号以高于奈奎斯特率的速率采样,则可以恢复原始信号。下图说明了如果在频域中以高于2w的速率采样信号的情况。
如果以低于2w的速率对同一信号进行采样,则采样信号将如下面的图所示。
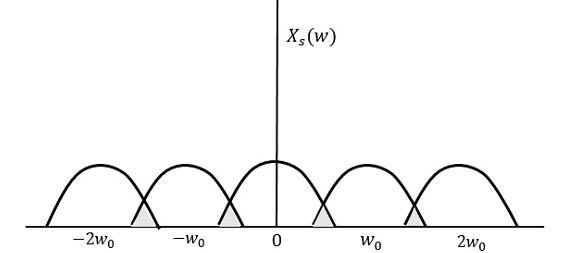
我们可以从上述模式中观察到,信息发生了重叠,这会导致信息混合和丢失。这种不希望发生的重叠现象称为混叠。
混叠可以指“信号频谱中高频分量在其采样版本的频谱中呈现为低频分量的现象。”
因此,选择信号的采样率为奈奎斯特率,如采样定理中所述。如果采样率等于最高频率的两倍(2W)。
这意味着,
$$f_s = 2W$$
其中,
fs = 采样频率
W 是最高频率
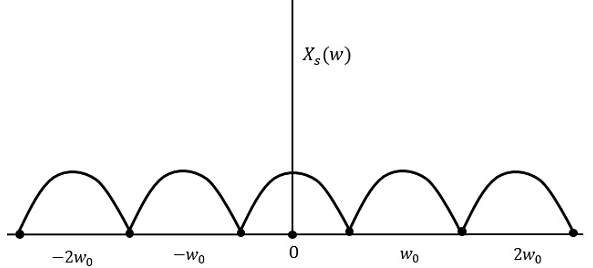
结果将如上图所示。信息被替换,没有任何损失。因此,这是一个良好的采样率。