卫星通信原理
卫星是一个围绕另一个天体以数学上可预测的路径(称为轨道)运行的天体。通信卫星只不过是太空中一个微波中继站,有助于电信、无线电和电视以及互联网应用。
中继器是一种电路,它会增强接收到的信号并重新传输。但在这里,此中继器充当转发器,它将传输信号的频段从接收到的频段更改。
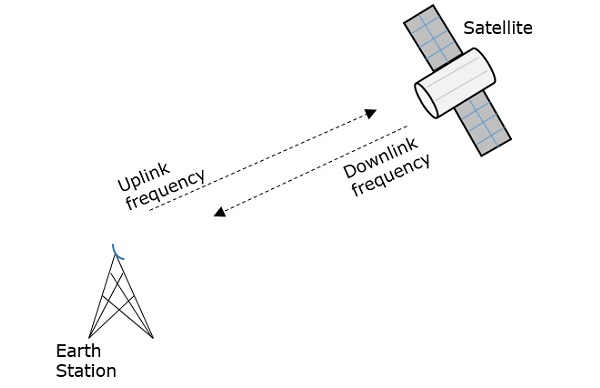
将信号发送到太空的频率称为上行链路频率,而转发器发送信号的频率称为下行链路频率。
下图清楚地说明了这一概念。
现在,让我们看看卫星通信的优点、缺点和应用。
卫星通信 - 优点
卫星通信有许多优点,例如 -
灵活性
安装新电路方便
轻松覆盖距离,成本无关紧要
广播可能性
覆盖地球的每个角落
用户可以控制网络
卫星通信 - 缺点
卫星通信具有以下缺点 -
初始成本(例如分段和发射成本)过高。
频率拥塞
干扰和传播
卫星通信 - 应用
卫星通信在以下领域得到应用 -
在广播中。
在电视广播中,例如DTH。
在互联网应用中,例如为数据传输提供互联网连接、GPS应用、互联网冲浪等。
用于语音通信。
用于许多领域的研发部门。
在军事应用和导航中。
卫星在其轨道上的方向取决于三个定律,称为开普勒定律。
开普勒定律
天文学家约翰内斯·开普勒(1571-1630)提出了 3 条关于卫星运动的革命性定律。卫星围绕其主星(地球)运行的路径为椭圆。椭圆有两个焦点 - F1 和 F2,地球是其中之一。
如果考虑从物体中心到其椭圆路径上某一点的距离,则椭圆离中心最远点称为远地点,椭圆离中心最近点称为近地点。
开普勒第一定律
开普勒第一定律指出:“每个行星都沿椭圆轨道绕太阳运行,太阳位于其一个焦点上。”因此,卫星沿以地球为一个焦点的椭圆路径运行。
椭圆的长半轴用“a”表示,短半轴用b表示。因此,该系统的偏心率 e 可以写成 -
$$e = \frac{\sqrt{a^{2}-b^{2}}}{a}$$
偏心率 (e) - 它是一个参数,定义了椭圆形状与圆形形状的差异。
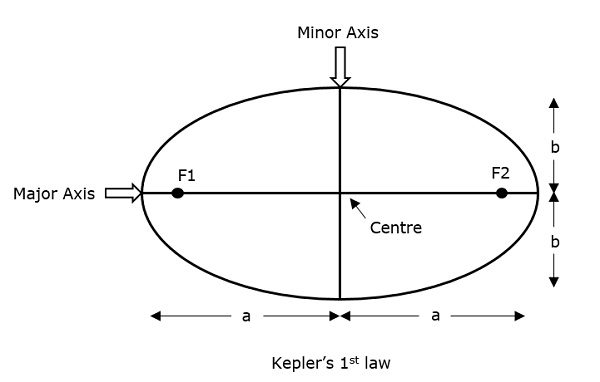
长半轴 (a) - 它是在中心沿两个焦点绘制的最长直径,与两个远地点(椭圆离中心最远点)相切。
短半轴 (b) - 它是在中心绘制的最短直径,与两个近地点(椭圆离中心最近点)相切。
这些在下图中得到了很好的描述。
对于椭圆路径,始终希望偏心率介于 0 和 1 之间,即 0 < e < 1,因为如果e变为零,路径将不再是椭圆形,而是会变成圆形路径。
开普勒第二定律
开普勒第二定律指出:“在相等的时间间隔内,卫星覆盖的面积相对于地球中心相等。”
可以通过查看下图来理解。
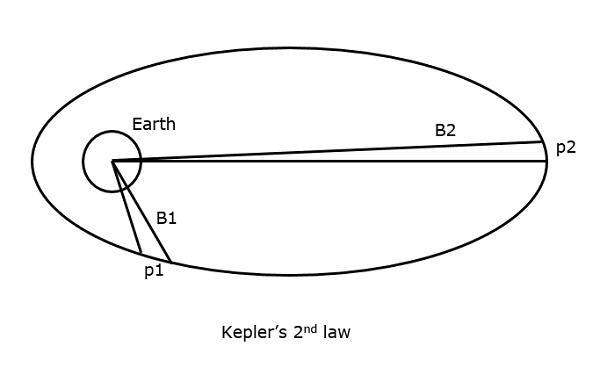
假设卫星在相同的时间间隔内覆盖p1和p2距离,则在这两种情况下分别覆盖的面积B1和B2相等。
开普勒第三定律
开普勒第三定律指出:“轨道的周期时间的平方与两个天体之间平均距离的立方成正比。”
这可以用数学方式写成
$$T^{2}\:\alpha\:\:a^{3}$$
这意味着
$$T^{2} = \frac{4\pi ^{2}}{GM}a^{3}$$
其中 $\frac{4\pi ^{2}}{GM}$ 是比例常数(根据牛顿力学)
$$T^{2} = \frac{4\pi ^{2}}{\mu}a^{3} $$
其中 μ = 地球的地球中心引力常数,即 Μ = 3.986005 × 1014 m3/sec2
$$1 = \left ( \frac{2\pi}{T} \right )^{2}\frac{a^{3}}{\mu}$$
$$1 = n^{2}\frac{a^{3}}{\mu}\:\:\:\Rightarrow \:\:\:a^{3} = \frac{\mu}{n^{2}}$$
其中n = 卫星的平均运动,单位为弧度/秒
卫星的轨道运行是借助这些开普勒定律计算出来的。
除此之外,还有一件重要的事情需要注意。卫星绕地球运行时,会受到地球的引力。此外,它还会受到太阳和月球的一些引力。因此,它受到两个力的作用。它们是 -
向心力 - 倾向于将沿轨迹路径运动的物体拉向自身的力称为向心力。
离心力 - 倾向于将沿轨迹路径运动的物体推离其位置的力称为离心力。
因此,卫星必须平衡这两个力才能保持在轨道上。
地球轨道
当卫星发射到太空时,需要将其放置在某个轨道上,为其旋转提供特定的方式,以便保持可访问性并发挥其科学、军事或商业用途。这些分配给卫星的轨道相对于地球称为地球轨道。这些轨道上的卫星是地球轨道卫星。
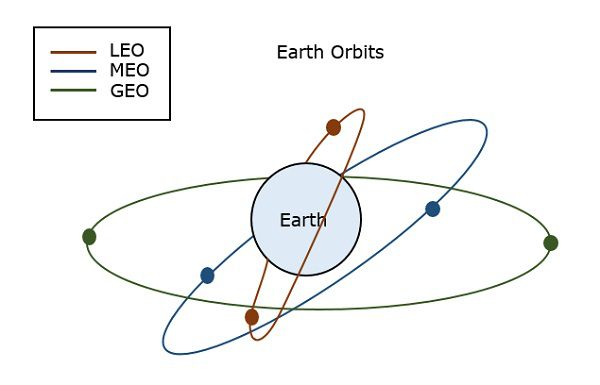
地球轨道的常见类型有 -
地球同步轨道
中地球轨道
低地球轨道
地球同步轨道卫星
地球同步轨道 (GEO) 卫星是指放置在地球上方 22,300 英里高度的卫星。该轨道与恒星日(即 23 小时 56 分钟)同步。此轨道可能具有倾角和偏心率。它可能不是圆形的。该轨道可以倾斜于地球的两极。但从地球上观察时,它看起来是静止的。
如果相同的地球同步轨道是圆形的并且位于赤道平面内,则称为地球静止轨道。这些卫星放置在地球赤道上方 35,900 公里(与地球同步轨道相同)的高度,并且它们相对于地球的方向(西到东)不断旋转。这些卫星被认为相对于地球是静止的,因此名称也暗示了这一点。
地球静止轨道卫星用于天气预报、卫星电视、卫星广播和其他类型的全球通信。
下图显示了地球同步轨道和地球静止轨道的区别。旋转轴表示地球的运动。
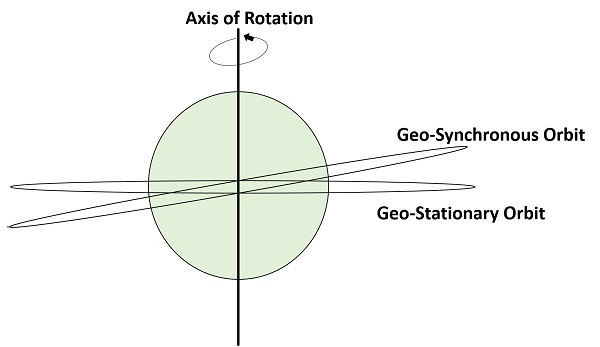
注意 - 每个地球静止轨道都是地球同步轨道。但并非每个地球同步轨道都是地球静止轨道。
中地球轨道卫星
中地球轨道 (MEO) 卫星网络将在地球表面约 8000 英里的距离上运行。从 MEO 卫星传输的信号传播的距离较短。这转化为接收端增强的信号强度。这表明在接收端可以使用更小、更轻的接收终端。
由于信号到卫星和从卫星到接收站的传播距离较短,因此传输延迟较小。传输延迟可以定义为信号到达卫星并返回接收站所需的时间。
对于实时通信,传输延迟越短,通信系统越好。例如,如果 GEO 卫星往返需要 0.25 秒,那么 MEO 卫星完成相同行程需要不到 0.1 秒。MEO 在 2 GHz 及以上频率范围内工作。
低地球轨道卫星
低地球轨道 (LEO) 卫星主要分为三类,即小型 LEO、大型 LEO 和巨型 LEO。LEO 将在地球表面上方 500 到 1000 英里的距离上运行。
这种相对较短的距离将传输延迟缩短至仅 0.05 秒。这进一步减少了对灵敏且笨重的接收设备的需求。小型 LEO 将在 800 MHz(0.8 GHz)范围内运行。大型 LEO 将在 2 GHz 或更高频率范围内运行,而巨型 LEO 在 20-30 GHz 频率范围内运行。
与巨型 LEO相关的较高频率转化为更大的信息承载能力,并产生实时、低延迟视频传输方案的能力。
下图描绘了 LEO、MEO 和 GEO 的路径。