数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学以字符串形式表示的树中第 k 层节点的乘积 (C++)
给定一个以字符串格式表示节点数据的树，任务是找到二叉树中第 k 层节点的乘积。树的每个节点包含三个部分：数据部分、指向左子树的左指针和指向右子树的右指针。
二叉树的层级从 0 开始，可以到任何正数 'n'。因此，给定层级 'k'，程序必须计算给定 'k' 层节点的乘积。
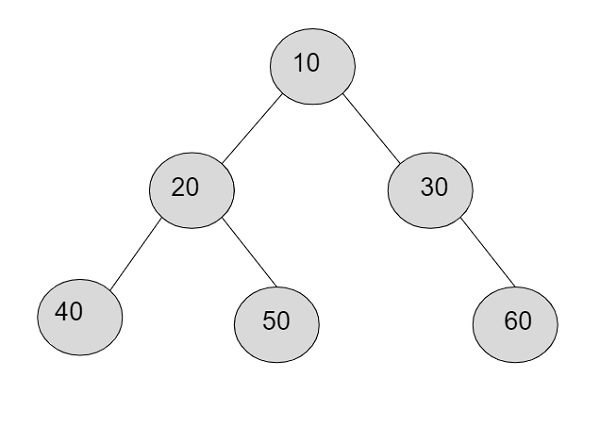
例如，在二叉树中，如果给定 k=2
则第 2 层的节点为 - 40, 50, 60
乘积 = 40 * 50 * 60 = 120000
输入
(1(2(3()())(4()(5()())))(6(7()())(8()()))) K = 1
输出
product of nodes at level k = 12
输入
(0(5(6()())(4()(9()())))(7(1()())(3()())))" k = 2
输出
product of nodes at level k = 72
算法
Start
Step 1→ Declare function to calculate nodes at k-th level
int product(string tree, int k)
Declare int level = -1
Declare int product = 1
Declare int size = tree.length()
Loop For int i = 0 and i < size and i++
IF tree[i] = '('
Set level++
End
Else IF tree[i] = ')'
Set level—
End
Else
IF level = k
Set product *= (tree[i] - '0')
End
End
End
return product
Step 2→ In main()
Declare string tree = "(1(2(3()())(4()(5()())))(6(7()())(8()())))"
Declare int k = 1
Call product(tree, k)
Stop示例
#include <bits/stdc++.h>
using namespace std;
//finding product at kth level
int product(string tree, int k){
int level = -1;
int product = 1;
int size = tree.length();
for (int i = 0; i < size; i++){
if (tree[i] == '(')
level++;
else if (tree[i] == ')')
level--;
else{
if (level == k)
product *= (tree[i] - '0');
}
}
return product;
}
int main(){
string tree = "(1(2(3()())(4()(5()())))(6(7()())(8()())))";
int k = 1;
cout <<"product of nodes at level k = "<<product(tree, k);
return 0;
}输出
运行以上代码将生成以下输出：
product of nodes at level k = 12
更新于：2020年8月13日
88 次浏览
广告