数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++程序中树的祖先-后代关系查询
在这个问题中，我们给定一个 N 个顶点的树和 Q 个查询，每个查询包含两个值 i 和 j。我们的任务是创建一个程序来解决树中祖先-后代关系的查询。
为了解决每个查询，我们需要检查节点 i 是否是树中节点 j 的祖先。
让我们举个例子来理解这个问题，
输入
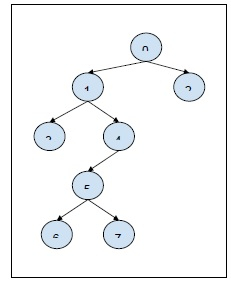
Q = 2, query[][] = {{3, 5}, {1, 6}}输出
No Yes
解释
i = 3, j = 5: The node 3 is not the ancestor of node 5. Return NO. i = 1, j = 6: The node 1 is the ancestor of node 6. Return YES.
解决方案方法
解决这个问题的一种方法是使用树遍历技术，即深度优先搜索（DFS）。我们将从第 i 个节点开始遍历，向下遍历到其所有后代，然后检查第 j 个节点是否是其后代。解决这个问题的一个有效方法是找出每个节点的进入时间和退出时间。并检查它们是否共享祖先-后代关系。
程序说明我们解决方案的工作原理，
示例
#include <bits/stdc++.h>
using namespace std;
void depthFirstSearch(vector<int> g[], int u, int parent, int entTime[], int exitTime[], int& cnt){
entTime[u] = cnt++;
for (int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if (v != parent) depthFirstSearch(g, v, u, entTime, exitTime, cnt);
}
exitTime[u] = cnt++;
}
void calcTimeInAndOut(int edges[][2], int V, int entTime[], int exitTime[]){
vector<int> g[V];
for (int i = 0; i < V - 1; i++) {
int u = edges[i][0];
int v = edges[i][1];
g[u].push_back(v);
g[v].push_back(u);
}
int cnt = 0; depthFirstSearch(g, 0, -1, entTime, exitTime, cnt);
}
int main(){
int edges[][2] = { { 0, 1 }, { 0, 2 }, { 1, 3 }, { 1, 4 }, { 4, 5 }, { 5, 6 }, { 5, 7 }};
int E = sizeof(edges) / sizeof(edges[0]);
int V = E + 1;
int Q = 2;
int query[Q][2] = {{3, 5}, {1, 6}};
int entTime[V], exitTime[V];
calcTimeInAndOut(edges, V, entTime, exitTime);
for(int i = 0; i < Q; i++){
cout<<"For query "<<(i+1)<<" : "; (entTime[query[i][0]] <= entTime[query[i][1]] && exitTime[query[i][0]] <= exitTime[query[i][1]])? cout<<"is Ancestor\n":cout<<"is not Ancestor\n";
}
return 0;
}输出
For query 1 : is Ancestor For query 2 : is not Ancestor
更新于: 2020年12月22日
196 次查看
广告