使用Python查找二叉树的最低公共祖先的程序

假设我们给定一棵二叉树以及两个特定的节点x和y。我们必须从二叉树中找出这两个节点的最低公共祖先。二叉树中最低的公共祖先是指x和y节点都是其后代的最低节点。此外，特定节点也可以是其自身的后代。我们必须找到该节点并将其作为输出返回。

因此，如果输入类似于

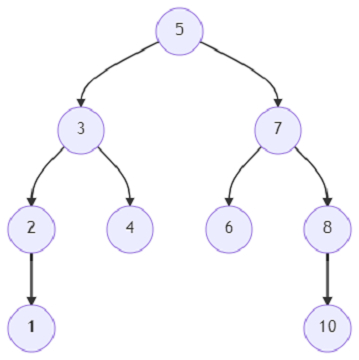
并且x = 2，y = 4；则输出将为3。

节点2和4的后代节点是3。因此，将返回3。

为了解决这个问题，我们将遵循以下步骤：

  • 定义一个函数dfs()。这将接收节点作为参数。

    • 如果节点类似于null，则

      • 返回

    • 如果节点存在于列表[x,y]中，则

      • left := dfs(节点的左子节点)

      • right := dfs(节点的右子节点)

      • 如果left或right非零，则

        • ans := 节点

        • 返回节点

    • left := dfs(节点的左子节点)

    • right := dfs(节点的右子节点)

    • 如果left和right均不为null，则

      • ans := 节点

      • 返回节点

    • 返回left或right

  • ans := dfs(根节点)

  • 返回ans


示例

 在线演示

class TreeNode:
def __init__(self, data, left = None, right = None):
   self.data = data
   self.left = left
   self.right = right
def insert(temp,data):
   que = []
   que.append(temp)
   while (len(que)):
      temp = que[0]
      que.pop(0)
      if (not temp.left):
      if data is not None:
         temp.left = TreeNode(data)
      else:
         temp.left = TreeNode(0)
         break
      else:
         que.append(temp.left)
      if (not temp.right):
      if data is not None:
         temp.right = TreeNode(data)
      else:
         temp.right = TreeNode(0)
         break
      else:
         que.append(temp.right)
def make_tree(elements):
   Tree = TreeNode(elements[0])
   for element in elements[1:]:
      insert(Tree, element)
      return Tree
def search_node(root, element):
   if (root == None):
      return None
   if (root.data == element):
      return root
      res1 = search_node(root.left, element)
   if res1:
      return res1
      res2 = search_node(root.right, element)
      return res2
def solve(root, x, y):
def dfs(node):
   if not node:
      return
   if node in [x,y]:
      left = dfs(node.left)
      right = dfs(node.right)
   if left or right:
      ans = node
      return node
      left = dfs(node.left)
      right = dfs(node.right)
   if left and right:
      ans = node
      return node
      return left or right
      ans = dfs(root)
   return ans
root = make_tree([5, 3, 7, 2, 4, 1, 7, 6, 8, 10])
print(solve(root, search_node(root, 2), search_node(root, 4)).data)

输入

make_tree([5, 3, 7, 2, 4, 1, 7, 6, 8, 10]),
search_node(root, 2),
search_node(root, 4)

输出

3

更新于：2021年5月28日

117 次浏览

启动您的职业生涯

完成课程后获得认证

开始
广告