数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究关于一点绕另一点旋转180度后的反射
你如何理解标题“关于一点绕另一点旋转180度后的反射”？让我们在这篇文章中解读它。
假设我们在二维平面上有两个点 (x1, y1) 和 (x2, y2)。
其中 (x2, y2) 是旋转点，(x1, y1) 是要反射的点。
现在，假设 x1,y1 绕 x2,y2 旋转 180 度，我们得到 x1`,y1`。
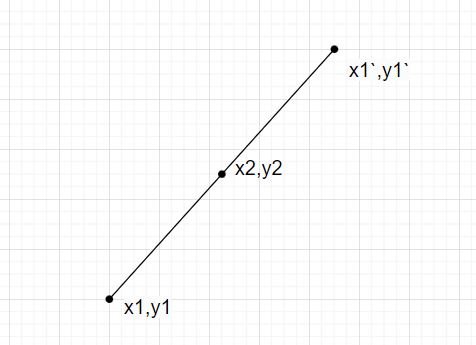
现在，我们可以观察到，如果我们在二维平面上给出两个点，其中一个点绕另一个点旋转，则会得到三个共线点，并且旋转点的另一个点也位于连接这三个点的直线的中间。
基于这些观察结果，我们可以使用以下步骤来找到反射点的坐标。
计算要反射的点和旋转点之间的差值。也就是说，计算 (x1−x2) 和 (y1−y2)。
要反射该点，我们需要将该差值添加到旋转点。也就是说，反射点将是 (x2+(x2−x1), y2+(y2−y1))。
简化方程，我们得到反射点为 (2x2−x1, 2y2−y1)。
因此，要反射一点 (x1, y1) 绕另一点 (x2, y2) 旋转 180 度，我们需要使用方程 (2x2−x1, 2y2−y1) 计算反射点。
例如，假设我们有一个点 (4, 6)，需要绕另一个点 (2, 2) 旋转 180 度进行反射。反射点可以计算为 (2*2−4, 2*2−6)，即 (0, −2) 或简化后的 (0, 2)。
方法
现在，我们对解决这个问题的逻辑有了清晰的认识。让我们记下将讨论的逻辑转换为程序的分步方法。
将两个点的坐标作为用户输入。
使用公式 (x2+(x2−x1), y2+(y2−y1)) 计算反射点的坐标。
将反射点打印到控制台。
C++ 代码实现
纸上得来终觉浅，绝知此事要躬行。现在让我们来写一些代码。
这是查找一点绕另一点旋转180度后的反射坐标的 C++ 实现。
示例
#include <iostream>
#include <cmath>
using namespace std;
int main() {
double x1 = 0;
double y1 = 0;
double x2 = 1;
double y2 = 1;
// Calculate the coordinates of the reflected point
double xr = x2 + (x2 - x1);
double yr = y2 + (y2 - y1);
cout << "The reflection of point (" << x1 << ", " << y1 << ") at 180-degree rotation of point (" << x2 << ", " << y2 << ") is (" << xr << ", " << yr << ").";
return 0;
}
输出
The reflection of point (0, 0) at 180-degree rotation of point (1, 1) is (2, 2).
空间复杂度：O(1)
时间复杂度：O(1)
结论
在这篇文章中，我们介绍了计算反射点坐标的逻辑，即一点绕另一点旋转180度后的反射，给定两个点。希望您对所涉及的概念和执行的代码有清晰的了解。
172 次浏览
