反射角

---

简介

角是两条相交直线之间旋转的角度。角可以有多种类型，例如锐角、直角、钝角等。其中一种角是反射角。反射角是两条直线之间角度的反射。由于我们无法使用量角器测量大于 180° 的角，因此我们可以借助反射角来测量角度。在本教程中，我们将学习角、角的类型、反射角、凹多边形、现实生活中的反射角以及一些关于反射角的解题示例。

角

角定义为二维几何中两条直线或射线之间旋转的角度。角也可以定义为从同一点发出的两条射线之间形成的角度变化。

角的类型

根据角的大小，可以将角划分为不同的类别。

• 锐角 - 如果两条直线相交形成小于 90 度的角，则该角称为锐角。

• 直角 - 如果两条直线相交形成 90 度的角，则该角称为直角。

• 钝角 - 如果两条直线相交形成大于 90 度的角，则该角称为钝角。

• 平角 - 如果两条直线相交形成等于 180 度的角，则所成的角称为平角。

• 反射角 - 如果两条直线相交形成大于 180 度小于 360 度的角，则该角称为反射角。

• 周角 - 如果两条直线相交形成等于 360 度的角，则该角称为周角。

反射角

反射角是两条直线之间形成的角度，它是主角的反射。反射角的旋转角度可以在 180° 到 360° 之间。一个角与其反射角一起构成一个周角。我们知道周角是 360°，对于一个角 x，相应的反射角将是 360-x。

下图给出了一个反射角。该图显示了两条直线之间的角度及其对应的反射角，两者结合构成一个周角。反射角有助于我们确定大于 180° 的角度。

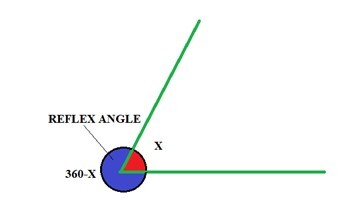
在给定一个角 x 的情况下，要找到反射角，我们可以从 360° 中减去角 x。

假设给定的角为 x，如上图所示。

我们知道周角为 360°。

因此，反射角 = 360°-x

凹多边形

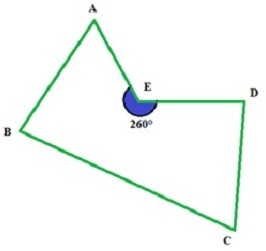
有一个或多个内角大于 180° 的多边形称为凹多边形。

凹多边形至少有四条边，并且不能是正多边形。

另一方面，凸多边形是一个所有角都小于 180° 的多边形。因此，凹多边形与凸多边形相反。

如多边形图所示，其中一个角为 260°，大于 180°。

现实生活中的反射角

就像角一样，我们可以在日常生活中随处可见反射角。因为我们到处都能看到角，所以一定会有与角相关的反射角。一些例子有 -

• 时钟 - 模拟时钟是反射角的最佳例子之一，因为我们每天都在各个地方看到它。假设时钟敲响 3 点，我们知道时针和分针形成 90° 的角。因此，该角度之间的数字将是 1、2 和 3。而如果我们寻找反射角，则该角度将包括数字 4、5、6、7、8、9、10、11 和 12。

• 比萨 - 如果你看到一个比萨，它是一个圆形。当我们沿着它的中心将比萨切成块并取出一块时，空隙形成一个角，而剩下的比萨显示出它的反射角。

解题示例

1.对于一个角 $\mathrm{\angle AOB== 57^\circ}$，求反射角 $\mathrm{\angle AOB}$ 的值。

解：我们知道一个角及其反射角共同构成一个周角。因此，反射角可以通过以下公式计算

$$\mathrm{\angle AOB = 360^\circ - 57^\circ = 303^\circ.}$$

2.根据反射角的性质判断真或假。

• 反射角可以是钝角。

• 170° 是反射角。

• 反射角可以是周角

解

• 否，钝角小于 180°，而反射角应大于 180°。

• 错误，170° 不是反射角，因为它是一个钝角。

• 反射角不能是周角，因为周角是 360°，而反射角小于 360°。

3.给出反射角的例子。

解

我们知道反射角在 180° 和 360° 之间

因此，如果我们将锐角、直角或钝角加到平角上，就会得到反射角。

结论

角是两条相交直线之间旋转的角度。角可以有多种类型，例如锐角、直角、钝角等。其中一种角是反射角。反射角是两条直线之间形成的角度，它是主角的反射。反射角的旋转角度可以在 180° 到 360° 之间。有一个或多个内角大于 180° 的多边形称为凹多边形。另一方面，凸多边形是一个所有角都小于 180° 的多边形。模拟时钟是反射角的最佳例子之一。当我们沿着它的中心将比萨切成块时，剩下的比萨显示出它的反射角。

角的类型	描述
锐角	小于 90° 的角
直角	等于 90° 的角
钝角	大于 90° 的角
平角	等于 180° 的角
反射角	180° 和 360° 之间的角。
周角	等于 360° 的角。

常见问题

1. 反射角的一些例子是什么？

200°、225°、270° 和 315° 是一些反射角。

2. 什么是凸多边形？

凸多边形是一个所有内角都小于 180° 的多边形。

3. 什么是凹多边形？

凹多边形是一个至少有一个角大于 180° 的多边形。

4. 反射角与主角有什么区别？

主角不能大于 180°，而反射角总是大于 180°。

5. 求反射角的公式是什么？

反射角可以通过从 360° 中减去主角来获得。