数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究已知∠XYZ = 64°，XY 延长至点 P。根据所给信息画一个图形。如果射线 YQ 平分∠ZYP，求∠XYQ 和∠QYP 的优角。
已知
已知∠XYZ = 64°，XY 延长至点 P，射线 YQ 平分∠ZYP。
要求
我们必须根据所给信息画一个图形，并求∠XYQ 和∠QYP 的优角。
解答
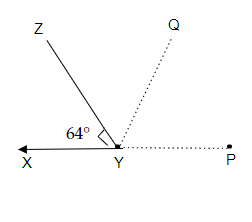
XYP 是一条直线。
因此，
∠XYZ + ∠ZYP = 180°
64° + ∠ZYP = 180° (因为∠XYZ = 64°)
这意味着，
∠ZYP = 180° - 64°
∠ZYP = 116°
因为，
YQ 平分∠ZYP
我们得到，
∠ZYQ = ∠QYP
并且，
∠ZYP = 2∠QYP
这意味着，
116° = 2∠QYP
116°/2 = ∠QYP
58° = ∠QYP
也就是说，
∠QYP = 58°
因此，
∠ZYQ = ∠QYP = 58°
类似地，我们得到，
∠XYQ = ∠XYZ + ∠ZYQ
这意味着，
∠XYQ = 64° + 58°
∠XYQ = 122°
现在让我们找到，
∠QYP 的优角
∠QYP = 180° + ∠XYQ (因为∠QYP 是∠XYQ 的优角)
我们有∠XYQ，代入后得到，
∠QYP = 180° + 122°
这意味着，
∠QYP = 302°。
因此，∠QYP = 302°。
更新于： 2022 年 10 月 10 日
49 次浏览
广告