弹性常数之间的关系

---

引言

根据物理学原理，建立三个弹性常数之间的联系可以得出它们之间适当的相互关系，这被称为“弹性常数”公式。根据“杨氏模量”（E）和“泊松比 (𝝂)”的定义，它们被理解为独立的“弹性常数”，可以通过适当的实验来确定它们之间的关系。本教程将阐述“弹性常数”之间的关系。

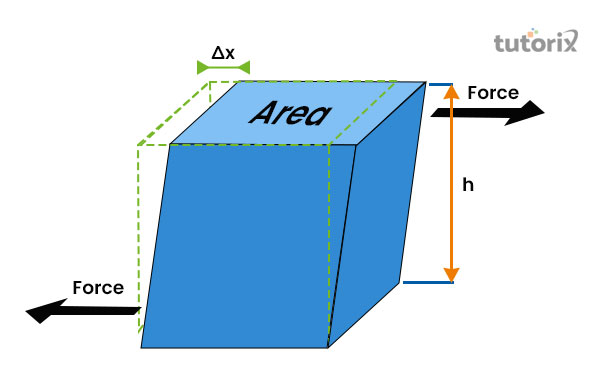
图1：“弹性常数”

弹性极限

当外力作用于物体时，物体往往会发生变形。在物理学中，这被称为“弹性体”。此外，那些在外力作用下发生变形，在外力移除后能够恢复到原始形状和大小的物体，其特性被称为弹性。在这种情况下，如果外力作用在一定限度内（Lkouniv.ac, 2022），物体就能恢复到原来的尺寸和形状。此外，这个限度内的力可以使变形完全消失，取决于所施加力的位移。此外，力的值近似于控制力的极限，该极限被称为物体的弹性极限。

弹性常数公式

当弹性体发生应力时，会产生与其成比例的应变。施加的应力与产生的应变的比率保持恒定，在物理学中被称为“弹性常数”。“弹性常数”可以用来理解物体的弹性行为 (Theconstructor, 2022)。“弹性常数”最常用的公式取决于三种不同的模量。理解“弹性常数”的基本公式是

$$\mathrm{E =\frac{应力}{应变}}$$

不同的弹性常数

“弹性常数”之间的关系和公式取决于施加的应力与产生的应变。弹性模量分为以下三种类型：

“杨氏模量 (E)”

根据胡克定律，当物体受到拉伸压力或应力时，在该物体的“弹性极限”内，施加的应力与应变成正比。应力与应变的比率是常数。这个关系和公式被称为杨氏模量或“弹性模量”（Hasan, Rosli & Alkahari, 2020）。“杨氏模量”用字母“E”表示。

“体积模量 (K)”

当物体受到垂直方向的均匀压力并产生正应力时，应力与应变的比率保持恒定。根据该定律，弹性常数的定义是正应力与相应的体积应变之比保持恒定。“体积模量”用字母“K”表示。可以使用以下公式计算体积模量：

$$\mathrm{K = \frac{正应力}{体积应变}}$$

(Yuan et al. 2019)。体积模量的一个关键点是，它可以表示物体在承受压力时抵抗体积变化的能力。

剪切模量

剪切模量也称为“刚性模量”，用于定义物体弹性刚度的量度。根据这个模量，当物体受到相应的剪切应力时，物体的形状会发生改变。“G”字母代表“刚性模量”。

图2：工程参考中的“弹性常数”

弹性常数之间的关系

“弹性常数”是物理学中一个非常重要的主题，它可以通过三种模量来解释，即“杨氏模量、体积模量和剪切模量”。

理解应力和应变对于理解物体“弹性常数”的形成至关重要。作用在固体上的变形力会导致其尺寸发生变化。在这种情况下，可以使用弹性常数之间的关系来理解变形的幅度 (Mechcontent, 2022)。当移除外力后，物体可以恢复到原始的尺寸和形状。

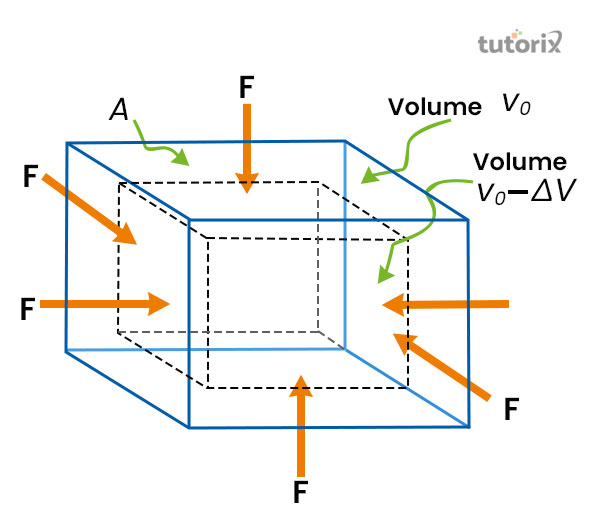
图3：弹性：应变和应力

胡克定律

胡克定律指出，当物体在弹性极限内，应力与应变成正比。这也指的是应力与应变的比率在弹性极限内是常数。

因此，常数的公式为 $\mathrm{\frac{应力}{应变}= 常数}$

结论

在本教程中，我们对变形力进行了全面的概述，这有助于了解应力和应变。此外，本教程的重点是与“弹性常数”的理解相关的不同模量。由于物体的弹性取决于施加的应力和应变，因此它可以随用于表示物体弹性和极限的不同比率而变化。

常见问题 (FAQs)

Q1。“弹性常数”是什么？

A1。“弹性常数”是帮助解释相关应力类型与其对应的应变之间关系的常数。

Q2。“弹性常数 K”是什么？

A2。在物理学中，弹簧常数用字母 K 表示。它也指显示与线性关系相关的行为的变化。

Q3。弹性中的“体积模量”是什么？

A3。“体积模量”是指测量压力增加时体积减少量的过程。此功能在很大程度上依赖于温度。

参考文献

期刊

Hasan, R., Rosli, N. A., & Alkahari, M. R. (2020). Elastic modulus approximation via experimental formulation for ABS lattice structure material. Proceedings of Mechanical Engineering Research Day, 2020, 51-52. Retrieved from: https://www3.utem.edu.my

Yuan, X., Zhu, X., Wang, C., & Zhang, L. (2019). Research on theoretical model of dynamic bulk modulus of gas-containing hydraulic oil. IEEE Access, 7, 178413-178422. Retrieved from: https://ieeexplore.ieee.org/iel7/6287639/8600701/08931608.pdf

网站

Lkouniv.ac, (2022), 关于弹性常数, Retrieved from: https://www.lkouniv.ac.in [检索于 2022年6月10日]

Mechcontent, (2022), 关于弹性常数, Retrieved from: https://mechcontent.com/relation-elastic-constants/ [检索于 2022年6月10日]

Pressbooks.online, (2022), 关于弹性常数, Retrieved from: https://pressbooks.online.ucf.edu/algphysics/chapter/elasticity-stress-and-strain/ [检索于 2022年6月10日]

Theconstructor, (2022), 关于弹性常数, Retrieved from: https://theconstructor.org[检索于 2022年6月10日]