Logistic Regression 中 Log Odds 的作用

---

简介

Logistic Regression 是一种统计方法，用于根据一个或多个自变量之间关系预测因变量。它利用 log odds，并在逻辑函数的帮助下预测事件发生的概率。它是一种分类方法。

什么是 Log Odds 以及为什么它们对 Logistic Regression 有用？

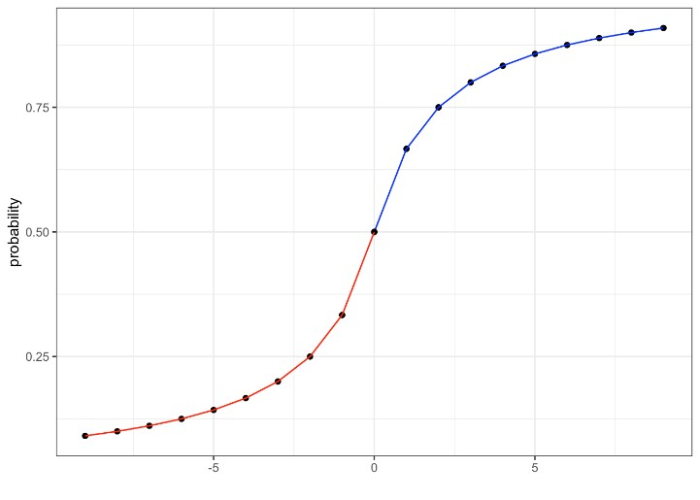
Logistic Regression 用于预测二元结果。例如，在选举中，候选人是否会获胜，短信是否是垃圾邮件等等。

Odds 是成功概率与失败概率的比率。它表示为

$$\mathrm{Odds \:=\: p\: / \:1- p}$$

其中 p = 成功概率，1 – p = 失败概率

log odds 将由以下公式给出

$\mathrm{Log \:of\: odds\: = \:log \:(p\: /\: 1 - p)}$                                                                           (1)

上述公式 (1) 是 logit 函数，表示为

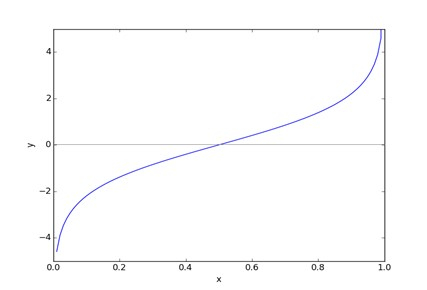
将此公式拟合到一条直线上，我们得到

$\mathrm{log\frac{p}{1-p}\:=\:\beta_0x\:+\:\beta_1x}$        [Logistic Regression 公式]           (2)

$\mathrm{p\:=\:\frac{e^{\beta_0x\:+\:\beta_1x}}{1\:+\:e^{\beta_0x\:+\:\beta_1x}}}$                       (3)

失败概率可以写成

$\mathrm{1-p\:=\:\frac{1}{1\:+\:e^{\beta_0x\:+\:\beta_1x}}}$                            (4)

Log Odds 比率可以写成

$\mathrm{p/1-p\:=\:\frac{1}{1\:+\:e^{\beta_0x\:+\:\beta_1x}}\:=\:e^{\beta_0x\:+\:\beta_1x}}$                 (5)

这是 Logistic Regression 的公式。

Python 中的 Odds Ratio 示例

让我们来看以下数据。

	国家1	国家2
猎豹	8	2
狮子	1	5

示例

from scipy.stats import fisher_exact as fe 
odds_ratio, p_value = fe([[8, 2], [1, 5]]) 
print(odds_ratio)

输出

20.0

Log Odds 的优点

• Log Odds 将基于概率的 Logistic Regression 模型转换为基于似然的模型。

• Logistic Regression 参数由最大似然估计 (MLE) 确定。

• 它们在解决胜负、欺诈与非欺诈、垃圾邮件与非垃圾邮件等场景中非常有用。

结论

当我们需要非二元结果时，Logistic Regression 中使用 Log Odds。Log Odds 使 Logistic Regression 能够同时用于回归和分类模型。