机器学习中逻辑回归的代价函数

---

简介

逻辑回归是机器学习中最简单的分类算法之一。逻辑回归使用对数损失或交叉熵损失作为损失函数，而不是均方误差。既然我们已经有了线性回归，为什么还需要逻辑回归进行分类，为什么不能使用线性回归进行分类呢？

让我们通过本文了解这一事实，并详细探讨逻辑回归中使用的代价函数。

为什么我们需要逻辑回归，而不能使用线性回归？

在线性回归中，我们预测的是一个连续值。如果我们将线性回归拟合到分类任务中，最佳拟合线看起来就像下面的图表。

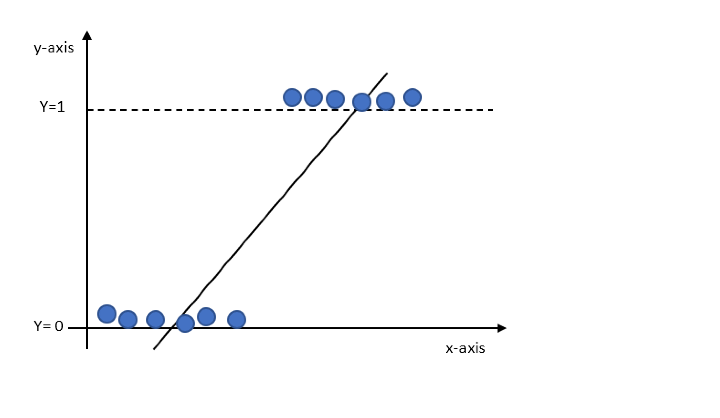
根据上图，我们将有大于1和小于0的值，但这对于分类来说是没有意义的，因为我们只对二元输出0或1感兴趣。

因此，我们需要值存在于Y=0和Y=1之间。需要转换上述直线，使值位于0和1之间。一种这样的转换是应用sigmoid函数，如下所示。

$$\mathrm{K=MX+c}$$

$$\mathrm{Y=F(K)}$$

$$\mathrm{F(K)=\frac{1}{1+e^{−Z}}}$$

$$\mathrm{Y=\frac{1}{1+e^{−Z}}}$$

该图现在如下所示

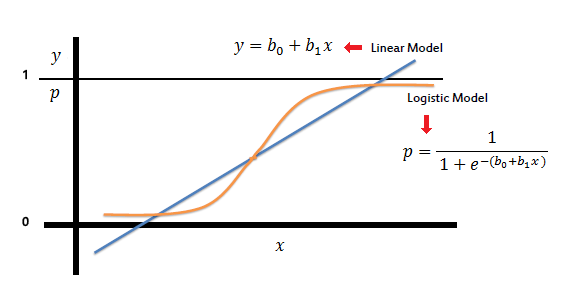
sigmoid函数给出0和1之间的连续值，这些值是概率值。

逻辑回归的对数损失和代价函数

使用概率评估分类模型的流行指标之一是对数损失。

$$\mathrm{F=−\sum_{i=1}^M\:y_{i}\log(p_{\theta}(x_{i}))+(1−y_{i})\log(1−p_{\theta}(x_{i}))}$$

代价函数可以写成

$$\mathrm{F(\theta)=\frac{1}{n}\sum_{i=1}^n\frac{1}{2}[p_{\theta}(x^{i})−Y^{i}]^{2}}$$

对于逻辑回归，

$$\mathrm{p_{\theta}(x)=g(\theta^{T}x)}$$

上述等式导致一个非凸函数，该函数充当代价函数。逻辑回归的代价函数是对数损失，总结如下。

$$\mathrm{cost(p_{\theta}(x),(y))=\left(\begin{array}{c}{−\log(p_{\theta}(x))\:if\:y=1}\ {−\log(1−p_{\theta}(x))\:if\:y=0}\end{array}\right)}$$

梯度下降更新方程变为：

$$\mathrm{\theta_{k}:=\theta_{k}−\alpha \sum_{i=1}^n[p_{\theta}(x^{i})−y^{i}]x_j^i}$$

结论

逻辑回归是最基本的分类算法。它使用对数损失或交叉熵损失作为代价函数，倾向于预测0和1之间的结果概率。