机器学习中的Python多项式回归

介绍

在多项式回归中，因变量Y和自变量X之间的关系被建模为多项式的n次方，这是一种线性回归。这样做是为了使用数据点绘制最佳拟合曲线。让我们在这篇文章中进一步探讨多项式回归。

多项式回归

多项式回归是多元线性回归模型的罕见情况之一。换句话说，当因变量和自变量之间存在曲线关系时，它是一种线性回归。它拟合数据中的多项式关系。

此外，通过包含多个多项式项，多个线性回归方程被转换成多项式回归方程。

在多项式回归中，自变量x和因变量y之间的关系被建模为n次多项式。多项式回归拟合自变量x的值与其条件均值y (用E(y|x)表示)之间的非线性关系。

多项式回归的必要性

以下是指定多项式回归需求的一些标准。

  • 如果像简单线性回归那样，将线性模型应用于线性数据集，则会产生良好的结果。但是，如果将此模型应用于非线性数据集而无需调整，则会计算出较差的结果。这些会导致误差率增加，准确性下降以及损失函数的增加。

  • 当数据点以非线性方式排列时，需要多项式回归。

  • 如果存在非线性模型并且我们尝试拟合线性模型，则线性模型将无法覆盖任何数据点。为了确保覆盖所有数据点，使用多项式模型。然而，对于大多数数据点，使用多项式模型时，曲线比直线更有效。

  • 如果我们尝试将线性模型拟合到曲线数据，则残差（Y轴）与预测变量（X轴）的散点图将显示中间区域的许多正残差。因此，在这种情况下它是不合适的。

多项式回归的应用

基本上，它们用于定义或枚举非线性现象。

  • 组织生长速率。

  • 流行病的进展。

  • 湖泊沉积物中碳同位素的分布。

回归分析的基本目标是根据自变量x的值对因变量y的估计值进行建模。在简单回归中，我们使用以下方程

y = a + bx + e

这里，因变量是y，自变量是a，b和e。

多项式回归类型

存在多种多项式回归，因为多项式方程的次数没有上限，可以高达n次方。例如，多项式方程的二次方通常被称为二次方程。如上所述，该次数有效，直到n次方，我们可以根据需要推导出任意多个方程。因此，多项式回归通常分类如下。

  • 当次数为1时，为线性。

  • 方程的次数为2，为二次。

  • 三次方，次数为3，依此类推。

例如，当根据合成发生的温度检查化学合成的输出时，此线性模型通常不起作用。在这种情况下，我们使用二次模型。

y = a+b1x+b2+b2+e

这里，误差率为e，y截距为a，y是x的因变量。

Python中的多项式回归实现

步骤1 - 导入数据集和库

导入必要的库以及用于多项式回归分析的数据集。

# Importing up the libraries
import numpy as nm
import matplotlib.pyplot as mplt
import pandas as ps
# Importing up the dataset
data = ps.read_csv('data.csv')
data

输出

   sno Temperature Pressure
0    1     0        0.0002
1    2     20       0.0012
2    3     40       0.0060
3    4     60       0.0300
4    5     80       0.0900
5    6     100      0.2700

步骤2 - 第二步将数据集分成两部分。

将数据集分成X和y两部分。X将包含第1列和第2列。y列将包含这两列。

X = data.iloc[:, 1:2].values
y = data.iloc[:, 2].values

步骤3 - 使用线性回归拟合数据集

拟合线性回归模型的两个组成部分。

from sklearn.linear_model import LinearRegressiondata
line2 = LinearRegressiondata()
line2.fit(X, y)

步骤4 - 将多项式回归拟合到数据集

将多项式回归模型拟合到X和Y两个组成部分。

from sklearn.preprocessing import PolynomialFeaturesdata
poly = PolynomialFeaturesdata(degree = 4)
X_polyn = polyn.fit_transform(X)
polyn.fit(X_polyn, y)
line3 = LinearRegressiondata()
line3.fit(X_polyn, y)

步骤5 - 在此步骤中，我们使用散点图来可视化线性回归的结果。

mplt.scatter(X, y, color = 'blue')
mplt.plot(X, lin.predict(X), color = 'red')
mplt.title('Linear Regression')
mplt.xlabel('Temperature')
mplt.ylabel('Pressure')
mplt.show()

输出

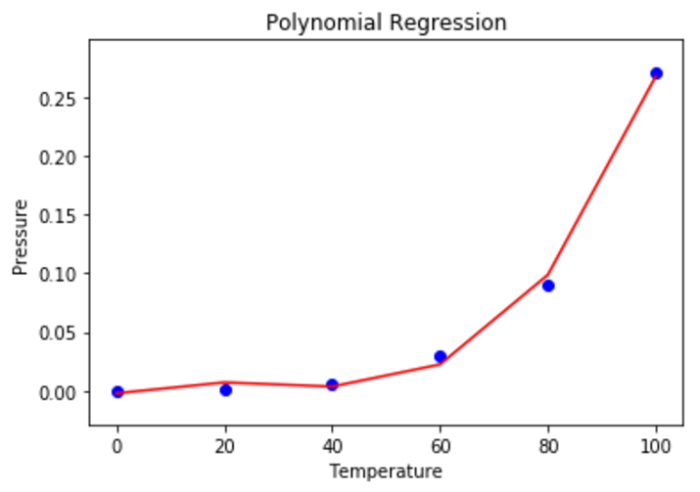
步骤6 - 使用散点图可视化多项式回归的结果。

mplt.scatter(X, y, color = 'blue')
mplt.plot(X, lin2.predict(polyn.fit_transform(X)), color = 'red')
mplt.title('Polynomial Regression')
mplt.xlabel('Temperature')
mplt.ylabel('Pressure')
mplt.show()

输出

步骤7 - 使用线性回归和多项式回归来预测未来的结果。需要注意的是，输入变量必须包含在一个NumPy 2D数组中。

线性回归

predic = 110.0
predicdarray = nm.array([[predic]])
line2.predict(predicdarray)

输出

Array([0.20657625])

多项式回归

Predic2 = 110.0
predic2array = nm.array([[predic2]])
line3.predicdict(polyn.fit_transform(predicd2array))

输出

Array([0.43298445])

优点

  • 它能够执行各种各样的任务。

  • 通常，多项式适合各种曲面。

  • 多项式提供了变量之间关系的最佳近似表示。

缺点

  • 它们对异常值非常敏感。

  • 一个或两个变量的存在可能会严重影响非线性分析的结果。

  • 此外，与线性回归相比，不幸的是，用于发现非线性回归中异常值的模型验证技术较少。

结论

在本文中，我们学习了多项式回归背后的理论。我们学习了多项式回归的实现。

在将此模型应用于真实数据集后，我们可以看到它的图形并使用它来进行预测。我们希望本节内容对您有所帮助，并且现在我们可以自信地将此知识应用于其他数据集。

更新于：2022年12月27日

940 次浏览

开启您的职业生涯

通过完成课程获得认证

开始学习
广告