机器学习中的简单线性回归
简介:简单线性回归
回归的“监督机器学习”算法用于预测连续特征。
最简单的回归程序,线性回归试图通过拟合一个线性方程或“最佳拟合线”到观察到的数据来解释因变量与一个或多个自变量之间的关系。
根据用作输入的特征数量,线性回归有两种版本
多元线性回归
简单线性回归
在本文中,我们将探讨简单线性回归的概念。
简单线性回归模型
简单线性回归是一种回归方法,它模拟给定自变量与因变量之间的关系。简单线性回归模型显示线性或倾斜的直线关系。
简单线性回归可以使用直线来建立两个变量之间的关系。绘制直线的第一个步骤是找到斜率和截距,它们都定义了直线并最小化回归误差。
简单线性回归的最基本版本由一个x变量和一个y变量组成。x变量是自变量,因为它不能被因变量预测。y变量是因变量,因为它是我们预测的依赖项。
简单线性回归的因变量必须具有连续或实数值。但是,自变量确实可以在连续或分类值上进行评估。
简单线性回归算法的两个主要目标如下
模拟两个变量之间的关系。例如,收入与支出、经验与薪酬等之间的关系。
预测新的观察结果。例如,根据温度预测天气,根据公司年度投资计算公司收入等。
下面的等式可以用来说明简单线性回归模型
y= a0+a1x+ ε
其中
回归线的截距,用符号a0表示,可以通过令x=0得到。
回归线的斜率,或a1,表示线是上升还是下降。
ε = 错误项。
SLR 算法的 Python 实现
在这里,我们采用一个包含两个变量的数据集:经验(自变量)和收入(因变量)。此问题的目标是 -
为了确定这两个变量是否相关,
将找到数据集的最佳拟合线。
自变量的变化如何影响因变量
在本节中,我们将构建一个简单线性回归模型,以确定哪条线最能代表这两个变量之间的关系。
在 Python 中实现简单线性回归模型需要执行以下步骤。
步骤 1:数据预处理
数据预处理是创建简单线性回归模型的第一步。本教程之前已经介绍过它。但是,将会有调整,如下面的步骤中所述 -
在导入数据集、构建图形和构建简单线性回归模型之前,我们将导入三个重要的库。
import numpy as np import matplotlib.pyplot as mtplt import pandas as ps
然后将数据集加载到我们的代码中。
data_set= ps.read_csv('Salarynov_Data.csv')
通过运行上面的代码(ctrl+ENTER),我们可以通过选择变量浏览器选项在我们的 Spyder IDE 屏幕上访问数据集。
输出中显示了数据集,其中包括两个变量经验和薪资。

然后必须从提供的数据集中提取因变量和自变量。工作经验是自变量,而薪资是因变量。代码如下
a= data_set.iloc[:, :-1].values b= data_set.iloc[:, 1].values
由于我们希望删除数据集的最后一列,因此我们在上面的代码行中将变量 a 的值设置为 -1。我们为变量 b 使用数字 1,因为我们希望提取第二列,因为索引从 0 开始。
然后将训练集和测试集分成两组。在我们拥有的总共 30 个观察值中,我们将使用 20 个观察值用于训练集,10 个观察值用于测试集。我们将数据集划分为训练集和测试集,以便我们可以使用一组进行训练,另一组进行测试我们的模型。
步骤 2. 将训练集拟合到 SLR
下一步是将我们的模型拟合到训练数据集。为此,我们将从 scikit-learn 线性模型包中导入 Linear Regression 类。在导入类之后,我们将创建一个回归器对象,它是该类的子类。
from sklearn.linear_model import LinearRegressionres regressor= LinearRegressionres() regressor.fit(a_train, b_train)
我们的因变量和自变量的训练数据集 x_train 和 y_train 已提供给 fit() 函数。为了使模型能够快速学习预测变量和目标变量之间的关系,我们将我们的回归器对象拟合到训练集。
步骤 3. 测试结果预测
薪资是因变量,然后是自变量(经验)。因此,我们的模型现在已准备好为新观察结果预测结果。在此阶段,我们将向模型提供一个测试数据集(新观察结果),以查看它是否可以预测所需的结果。
步骤 4. 可视化训练集的结果
将通过 scatter() 函数生成观察值的散点图。
我们将把员工的工作经验绘制在 x 轴上,并将他们的薪资绘制在 y 轴上。我们将向函数传递训练集的实际值——工作经验(x_train)、训练集的薪资(y_train)以及观察值的颜色。
现在我们需要绘制回归线,我们将使用 pyplot 库的 plot() 方法来做到这一点。将训练集的工作经验、训练集 x_pred 的预期收入和线条颜色传递给此函数。
然后将提供绘图的标题。在本例中,我们将名称“Salary vs Experience (Training Dataset)”传递给 Pyplot 模块的 title() 函数。
最后,我们将使用 show() 创建一个图形来描绘所有提到的内容。代码如下
mtplt.scatter(a_train, b_train, color="green") mtplt.plot(a_train, a_pred, color="red") mtplt.title("Salary vs Experience (Training Dataset)") mtplt.xlabel("Years of Experience") mtplt.ylabel("Salary(In Rupees)") mtplt.show()
输出
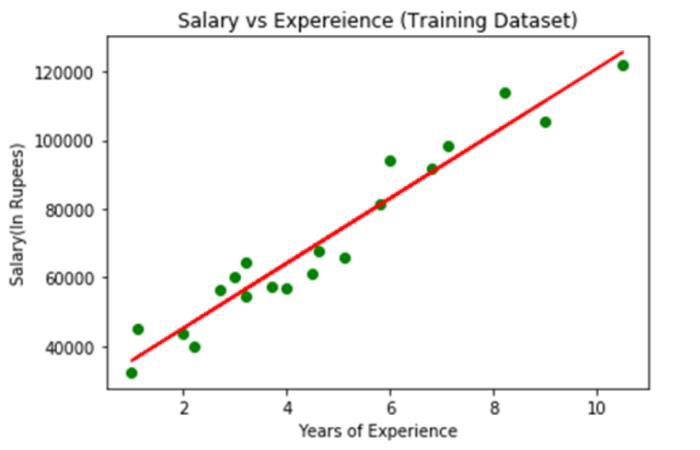
上图中,观察到的真实值以绿色点表示,而预期值则用红色回归线包围。回归线描绘了因变量和自变量的关系。
计算实际值和预期值之间的差距,可以了解线对数据的拟合程度。但是,正如我们从上图中看到的那样,大多数观察值都靠近回归线,因此我们的模型对训练集效果很好。
步骤 5. 显示测试集的结果
在前面的阶段,我们可视化了模型在训练集上的性能。现在我们将对测试集重复此过程。整个程序将与上面的程序相同,除了将使用 x_test 和 y_test 代替 x_train 和 y_train。
mtplt.scatter(a_train, b_train, color="blue") mtplt.plot(a_train, a_pred, color="red") mtplt.title("Salary vs Experience (Test Dataset)") mtplt.xlabel("Years of Experience") mtplt.ylabel("Salary(In Rupees)") mtplt.show()
输出

上图中蓝色表示观察值,红色回归线表示预测值。我们可以说我们的简单线性回归是一个可靠的模型,并且能够做出良好的预测,因为正如我们所看到的,大多数变量都靠近回归线。
结论
每个机器学习爱好者都必须熟悉线性回归算法,机器学习初学者应该从这里开始。它是一个相当简单但有用的算法。我们希望您发现这些信息有用。


 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP