数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究使用Python进行线性回归？
线性回归是机器学习中最简单且常用的工具之一，用于指示两个变量之间是否存在正相关或负相关关系。
线性回归是少数几个用于快速预测分析的优秀工具之一。在本节中，我们将使用python pandas包加载数据，然后估计、解释和可视化线性回归模型。
在我们深入探讨之前，让我们先讨论一下什么是回归？
什么是回归？
回归是一种预测建模技术，有助于建立因变量和自变量之间的关系。
回归类型
- 线性回归
- 逻辑回归
- 多项式回归
- 逐步回归
线性回归用于何处？
- 评估趋势和销售预测
- 分析价格变化的影响
- 评估风险
构建线性回归模型的步骤
首先，我们将构建设置并下载数据集和jupyter（我正在本教程中使用它，您可以使用其他IDE，如anaconda等）。
导入所需的包和数据集。
加载数据集后，我们将探索数据集。
将使用我们的数据集进行线性回归。
然后，我们将探索变量与一天中的时间之间的关系。
总结。
设置
您可以从以下链接下载数据集：
http://en.openei.org/datasets/dataset/649aa6d3-2832-4978-bc6e-fa563568398e/resource/b710e97d-29c9-4ca5-8137-63b7cf447317/download/building1retail.csv
我们将使用它来使用室外空气温度 (OAT) 作为解释变量来模拟建筑物的电力消耗。
将csv文件保存在jupyter或IDE安装的同一文件夹中。
导入所需的库和数据集
首先，我们将导入所需的库，然后使用pandas python库读取数据集。
# Importing Necessary Libraries
import pandas as pd
#Required for numerical functions
import numpy as np
from scipy import stats
from datetime import datetime
from sklearn import preprocessing
from sklearn.model_selection import KFold
from sklearn.linear_model import LinearRegression
#For plotting the graph
import matplotlib.pyplot as plt
%matplotlib inline
# Reading Data
df = pd.read_csv('building1retail.csv', index_col=[0],
date_parser=lambda x: datetime.strptime(x, "%m/%d/%Y %H:%M"))
df.head()输出
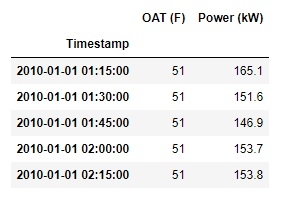
探索数据集
因此，让我们首先通过使用pandas绘制它来可视化我们的数据集。
df.plot(figsize=(22,6))
输出
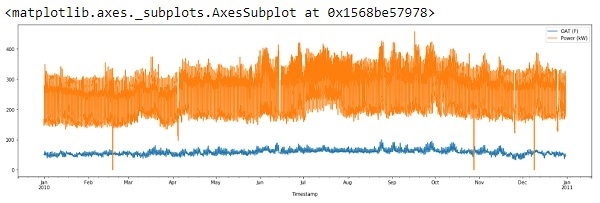
因此，x轴显示的是从2010年1月到2011年1月的数据。
如果我们看到上面的输出，我们可以注意到该图有两个奇怪的地方
似乎没有缺失数据，要检查它，只需运行
df.isnull().values.any()
输出
False
False结果告诉我们数据框中没有空值。
看来数据中有一些异常值（向下的长尖峰）。
异常值或“离群值”通常是实验错误的结果，也可能是真实值。无论哪种情况，我们都将丢弃它，因为它们会严重影响回归线的斜率。
在我们丢弃“离群值”之前，让我们首先检查一下我们的数据表示的是哪种类型的分布。
df.hist()
输出
从上面的直方图可以看出，我们的图表显示的数据大致遵循正态分布。
因此，让我们删除所有大于平均值 3 个标准差的值，并绘制新的数据框。
std_dev = 3 df = df[(np.abs(stats.zscore(df)) < float(std_dev)).all(axis=1)] df.plot(figsize=(22, 6))
输出
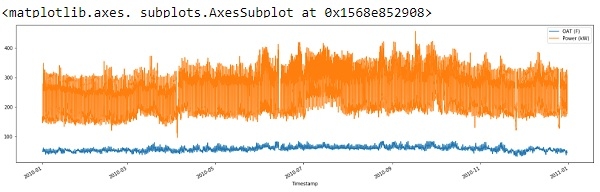
因此，从上面的输出中我们可以看到，我们已经在某种程度上消除了尖峰，并清理了我们的数据。
验证线性关系
为了找到OAT和电力之间是否存在任何线性关系，让我们绘制一个简单的散点图。
plt.scatter(df['OAT (F)'], df['Power (kW)'])
输出
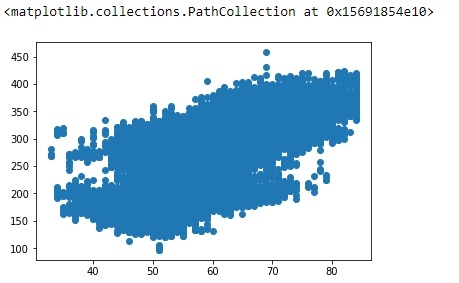
线性回归
为了运行模型并评估其性能，我们将使用Scikit-learn模块，我们还将使用k倍交叉验证（k=3）来评估模型的性能。
X = pd.DataFrame(df['OAT (F)']) y = pd.DataFrame(df['Power (kW)']) model = LinearRegression() scores = [] kfold = KFold(n_splits=3, shuffle=True, random_state=42) for i, (train, test) in enumerate(kfold.split(X, y)): model.fit(X.iloc[train,:], y.iloc[train,:]) score = model.score(X.iloc[test,:], y.iloc[test,:]) scores.append(score) print(scores)
输出
[0.38768927735902703, 0.3852220878090444, 0.38451654781487116]
在上面的程序中，model = LinearRegression() 创建了一个线性回归模型，for循环将数据集分成三折。然后在循环内，我们拟合数据，然后通过将其分数附加到列表中来评估其性能。
但是，结果看起来并不好，我们可以提高其性能。
一天中的时间
电力（变量）高度依赖于一天中的时间。让我们使用此信息通过使用独热编码将其合并到我们的回归模型中。
model = LinearRegression() scores = [] kfold = KFold(n_splits=3, shuffle=True, random_state=42) for i, (train, test) in enumerate(kfold.split(X, y)): model.fit(X.iloc[train,:], y.iloc[train,:]) scores.append(model.score(X.iloc[test,:], y.iloc[test,:])) print(scores)
输出
[0.8074246958895391, 0.8139449185141592, 0.8111379602960773]
我们的模型有了很大的改进。
总结
在本节中，我们学习了探索数据集并将其准备用于拟合回归模型的基础知识。我们评估了其性能，检测到了其缺点并对其进行了修复。
638 次浏览
