数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚学
法律学使用 PyTorch 进行线性回归？
线性回归简介
简单的线性回归基础
它让我们理解两个连续变量之间的关系。
示例 −
x = 自变量
体重
y = 因变量
身高
y = αx + β
让我们通过一个程序了解简单的线性回归 −
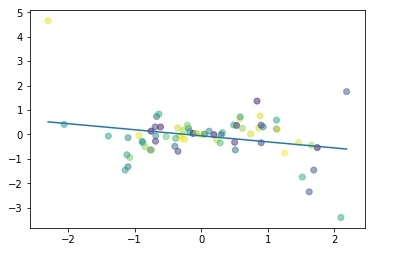
#Simple linear regression import numpy as np import matplotlib.pyplot as plt np.random.seed(1) n = 70 x = np.random.randn(n) y = x * np.random.randn(n) colors = np.random.rand(n) plt.plot(np.unique(x), np.poly1d(np.polyfit(x, y, 1))(np.unique(x))) plt.scatter(x, y, c = colors, alpha = 0.5) plt.show()
输出
线性回归的用途
最大程度地减少点和线 (y = αx + β) 之间的距离
调整
系数：α
切点/偏差：β
使用 PyTorch 构建线性回归模型
假设我们的系数 (α) 为 2，切点 (β) 为 1，则我们的方程将变为 −
y = 2x +1 # 线性模型
构建数据集
x_values = [i for i in range(11)] x_values
输出
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# 转换为 numpy
x_train = np.array(x_values, dtype = np.float32) x_train.shape
输出
(11,)
#Important: 2D required x_train = x_train.reshape(-1, 1) x_train.shape
输出
(11, 1)
y_values = [2*i + 1 for i in x_values] y_values
输出
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
#list iteration y_values = [] for i in x_values: result = 2*i +1 y_values.append(result) y_values
输出
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
y_train = np.array(y_values, dtype = np.float32) y_train.shape
输出
(11,)
#2D required y_train = y_train.reshape(-1, 1) y_train.shape
输出
(11, 1)
构建模型
#import libraries
import torch
import torch.nn as nn
from torch.autograd import Variable
#Create Model class
class LinearRegModel(nn.Module):
def __init__(self, input_size, output_size):
super(LinearRegModel, self).__init__()
self.linear = nn.Linear(input_dim, output_dim)
def forward(self, x):
out = self.linear(x)
return out
input_dim = 1
output_dim = 1
model = LinearRegModel(input_dim, output_dim)
criterion = nn.MSELoss()
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(), lr = learning_rate)
epochs = 100
for epoch in range(epochs):
epoch += 1
#convert numpy array to torch variable
inputs = Variable(torch.from_numpy(x_train))
labels = Variable(torch.from_numpy(y_train))
#Clear gradients w.r.t parameters
optimizer.zero_grad()
#Forward to get output
outputs = model.forward(inputs)
#Calculate Loss
loss = criterion(outputs, labels)
#Getting gradients w.r.t parameters
loss.backward()
#Updating parameters
optimizer.step()
print('epoch {}, loss {}'.format(epoch, loss.data[0]))输出
epoch 1, loss 276.7417907714844 epoch 2, loss 22.601360321044922 epoch 3, loss 1.8716105222702026 epoch 4, loss 0.18043726682662964 epoch 5, loss 0.04218350350856781 epoch 6, loss 0.03060017339885235 epoch 7, loss 0.02935197949409485 epoch 8, loss 0.02895027957856655 epoch 9, loss 0.028620922937989235 epoch 10, loss 0.02830091118812561 ...... ...... epoch 94, loss 0.011018744669854641 epoch 95, loss 0.010895680636167526 epoch 96, loss 0.010774039663374424 epoch 97, loss 0.010653747245669365 epoch 98, loss 0.010534750297665596 epoch 99, loss 0.010417098179459572 epoch 100, loss 0.010300817899405956
因此，我们可以看出从第 1 个历元到第 100 个历元，损失已大幅减少。
绘制图形
#Purely inference predicted = model(Variable(torch.from_numpy(x_train))).data.numpy() predicted y_train #Plot Graph #Clear figure plt.clf() #Get predictions predicted = model(Variable(torch.from_numpy(x_train))).data.numpy() #Plot true data plt.plot(x_train, y_train, 'go', label ='True data', alpha = 0.5) #Plot predictions plt.plot(x_train, predicted, '--', label='Predictions', alpha = 0.5) #Legend and Plot plt.legend(loc = 'best') plt.show()
输出
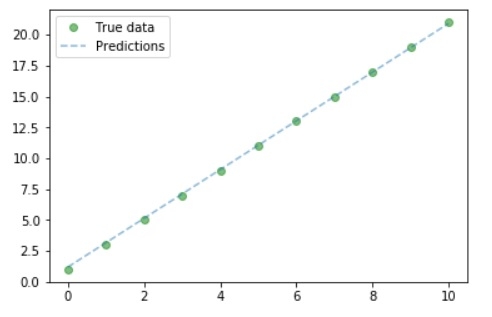
因此，我们可以从图形中看出我们的真实值和预测值非常相似。
更新于： 2019 年 7 月 30 日
493 次浏览
广告